题目内容
已知:如图,N、M是以O为圆心,1为半径的圆上的两点,B是 上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
(1)四边形EPGQ______(填“是”或者“不是”)平行四边形;
(2)若四边形EPGQ是矩形,求OA的值;
(3)连接PQ,求3PQ2+OA2的值.

(1)是.
证明:连接OB,如图①,

∵BA⊥OM,BC⊥ON,
∴∠BAO=∠BCO=90°,
∵∠AOC=90°,
∴四边形OABC是矩形.
∴AB∥OC,AB=OC,
∵E、G分别是AB、CO的中点,
∴AE∥GC,AE=GC,
∴四边形AECG为平行四边形.
∴CE∥AG,
∵点D、E、F、G分别是线段OA、AB、BC、CO的中点,
∴GF∥OB,DE∥OB,
∴PG∥EQ,
∴四边形EPGQ是平行四边形;
(2)解:如图②,

∵?EPGQ是矩形.
∴∠AED+∠CEB=90°.
又∵∠DAE=∠EBC=90°,
∴∠AED=∠BCE.
∴△AED∽△BCE,
∴ =
= ,
,
设OA=x,AB=y,则 :
: =
= :x,
:x,
得y2=2x2,
又∵OA2+AB2=OB2,
即x2+y2=12.
∴x2+2x2=1,
解得:x= .
.
即当四边形EPGQ是矩形时,OA的长度为 .
.
(3)解:如图③,连接GE交PQ于O′,

∵四边形EPGQ是平行四边形,
∴O′P=O′Q,O′G=0′E.
过点P作OC的平行线分别交BC、GE于点B′、A′.
由△PCF∽△PEG得, =
=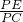 =
= =
= ,
,
∴PA′= A′B′=
A′B′= AB,GA′=
AB,GA′= GE=
GE= OA,
OA,
∴A′O′= GE-GA′=
GE-GA′= OA,
OA,
在Rt△PA′O′中,PO′2=PA′2+A′O′2,
即 =
= +
+ ,
,
又∵AB2+OA2=1,
∴3PQ2=AB2+ ,
,
∴OA2+3PQ2=OA2+(AB2+ )=
)= .
.
分析:(1)由BA⊥OM,BC⊥ON,∠AOC=90°,可判定四边形OABC是矩形,即可得AB∥OC,AB=OC,又由E、G分别是AB、CO的中点,即可得四边形AECG为平行四边形,连接OB,点D、E、F、G分别是线段OA、AB、BC、CO的中点,根据三角形中位线的性质,即可得PG∥EQ,即可判定四边形EPGQ是平行四边形;
(2)易得△AED∽△BCE,根据相似三角形的对应边成比例与勾股定理,即可求得OA的长;
(3)连接GE交PQ于O′,易得O′P=O′Q,O′G=0′E,然后过点P作OC的平行线分别交BC、GE于点B′、A′,由△PCF∽△PEG,根据相似三角形的对应边成比例与勾股定理,即可求得3PQ2+OA2的值.
点评:此题考查了相似三角形的判定与性质、平行四边形的判定与性质、矩形的判定与性质以及勾股定理等知识.此题综合性较强,难度较大,解题的关键是注意准确作出辅助线,注意数形结合思想与方程思想的应用.
证明:连接OB,如图①,

∵BA⊥OM,BC⊥ON,
∴∠BAO=∠BCO=90°,
∵∠AOC=90°,
∴四边形OABC是矩形.
∴AB∥OC,AB=OC,
∵E、G分别是AB、CO的中点,
∴AE∥GC,AE=GC,
∴四边形AECG为平行四边形.
∴CE∥AG,
∵点D、E、F、G分别是线段OA、AB、BC、CO的中点,
∴GF∥OB,DE∥OB,
∴PG∥EQ,
∴四边形EPGQ是平行四边形;
(2)解:如图②,

∵?EPGQ是矩形.
∴∠AED+∠CEB=90°.
又∵∠DAE=∠EBC=90°,
∴∠AED=∠BCE.
∴△AED∽△BCE,
∴
 =
= ,
,设OA=x,AB=y,则
 :
: =
= :x,
:x,得y2=2x2,
又∵OA2+AB2=OB2,
即x2+y2=12.
∴x2+2x2=1,
解得:x=
 .
.即当四边形EPGQ是矩形时,OA的长度为
 .
.(3)解:如图③,连接GE交PQ于O′,

∵四边形EPGQ是平行四边形,
∴O′P=O′Q,O′G=0′E.
过点P作OC的平行线分别交BC、GE于点B′、A′.
由△PCF∽△PEG得,
 =
=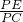 =
= =
= ,
,∴PA′=
 A′B′=
A′B′= AB,GA′=
AB,GA′= GE=
GE= OA,
OA,∴A′O′=
 GE-GA′=
GE-GA′= OA,
OA,在Rt△PA′O′中,PO′2=PA′2+A′O′2,
即
 =
= +
+ ,
,又∵AB2+OA2=1,
∴3PQ2=AB2+
 ,
,∴OA2+3PQ2=OA2+(AB2+
 )=
)= .
.分析:(1)由BA⊥OM,BC⊥ON,∠AOC=90°,可判定四边形OABC是矩形,即可得AB∥OC,AB=OC,又由E、G分别是AB、CO的中点,即可得四边形AECG为平行四边形,连接OB,点D、E、F、G分别是线段OA、AB、BC、CO的中点,根据三角形中位线的性质,即可得PG∥EQ,即可判定四边形EPGQ是平行四边形;
(2)易得△AED∽△BCE,根据相似三角形的对应边成比例与勾股定理,即可求得OA的长;
(3)连接GE交PQ于O′,易得O′P=O′Q,O′G=0′E,然后过点P作OC的平行线分别交BC、GE于点B′、A′,由△PCF∽△PEG,根据相似三角形的对应边成比例与勾股定理,即可求得3PQ2+OA2的值.
点评:此题考查了相似三角形的判定与性质、平行四边形的判定与性质、矩形的判定与性质以及勾股定理等知识.此题综合性较强,难度较大,解题的关键是注意准确作出辅助线,注意数形结合思想与方程思想的应用.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
 交⊙O于F,GF切⊙O于F且与CP交于G,CH切⊙O于C且与AB的延长线交于H,如果GP2=GD•GC,AD平分∠BAP并交HP于M.
交⊙O于F,GF切⊙O于F且与CP交于G,CH切⊙O于C且与AB的延长线交于H,如果GP2=GD•GC,AD平分∠BAP并交HP于M.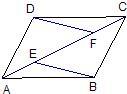 24、已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
24、已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.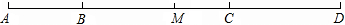
 已知:如图正方形ABCD,E是BC的中点,F在AB上,且BF=
已知:如图正方形ABCD,E是BC的中点,F在AB上,且BF= 已知:如图,A、C是?DEBF的对角线EF所在直线上的两点,且AE=CF.
已知:如图,A、C是?DEBF的对角线EF所在直线上的两点,且AE=CF.