Question

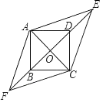
【题目】如图，四边形ABCD是边长为1的正方形，E，F为BD所在直线上的两点．若AE= ，∠EAF=135°，则以下结论正确的是（ ）

A. DE=1 B. tan∠AFO= C. AF= D. 四边形AFCE的面积为

Answer 1

【答案】C

【解析】

试题解析：∵四边形ABCD是正方形，∴AB=CB=CD=AD=1，AC⊥BD，∠ADO=∠ABO=45°，

∴OD=OB=OA=，∠ABF=∠ADE=135°，

在Rt△AEO中，EO=,∴DE= ，故A错误；

∵∠EAF=135°，∠BAD=90°，∴∠BAF+∠DAE=45°，∵∠ADO=∠DAE+∠AED=45°，∴∠BAF=∠AED，

∴△ABF∽△EDA，∴ ，∴ ，∴BF=，

在Rt△AOF中，AF= ，故C正确；

tan∠AFO= ，故B错误；

∴S四边形AECF=ACEF=××= ，故D错误；

故选C．