题目内容
如图,图中的曲线表示小华星期天骑自行车外出离家的距离与时间的关系 ,小华八点离开家,十四点回到家,根据这个曲线图,请回答下列问题:
,小华八点离开家,十四点回到家,根据这个曲线图,请回答下列问题:(1)到达离家最远的地方是几点?离家多远?
(2)何时开始第一次休息?休息多长时间?
(3)小华在往返全程中,在什么时间范围内平均速度最快?最快速度是多少?
(4)小华何时离家21千米?(写出计算过程)
分析:(1)图中的点的横坐标表示时间,所以点E点距离家最远,横坐标表示距家最远的时间,纵坐标表示离家的距离;
(2)休息是路程不在随时间的增加而增加;
(3)往返全程中回来时候平均速度最快;
(4)求得线段DE所在直线的解析式,令y=21解得x的值就是离家21千米的相应的时间.
(2)休息是路程不在随时间的增加而增加;
(3)往返全程中回来时候平均速度最快;
(4)求得线段DE所在直线的解析式,令y=21解得x的值就是离家21千米的相应的时间.
解答:解:(1)到达离家最远的地方是11点,此时距离家30千米;
(2)到距家17千米的地方开始休息,休息了(10-9.5)=0.5小时;
(3)小华在返回的途中最快,平均速度为30÷(14-12)=15千米/小时;
(4)由图象可知点D、E的坐标分别为(10,17),(11,30),F、G的坐标分别为(12,30),(14,0),
∴设直线DE所在直线的解析式为y=kx+b,直线FG的解析式为y=ax+c,
∴
,
,
解得:
,
,
∴解析式为y=13x-113,y=-15x+210,
令y=21,
解得:x=
或
,
∴第
或
时离家21千米.
(2)到距家17千米的地方开始休息,休息了(10-9.5)=0.5小时;
(3)小华在返回的途中最快,平均速度为30÷(14-12)=15千米/小时;
(4)由图象可知点D、E的坐标分别为(10,17),(11,30),F、G的坐标分别为(12,30),(14,0),
∴设直线DE所在直线的解析式为y=kx+b,直线FG的解析式为y=ax+c,
∴
|
|
解得:
|
|
∴解析式为y=13x-113,y=-15x+210,
令y=21,
解得:x=
| 134 |
| 13 |
| 189 |
| 15 |
∴第
| 134 |
| 13 |
| 189 |
| 15 |
点评:本题考查了一次函数的相关知识,是一道比较典型的函数综合题,考查了学生综合运用知识的能力.

练习册系列答案
相关题目
据统计每年由于汽车超速行驶而造成的交通事故是造成人员死亡的主要原因之一.行驶中的汽车,在刹车后由于惯性的原因,还要继续向前滑行一段距离才能停住,这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能(车速不超过140千米/时),对这种汽车的刹车距离进行测试,测得的数据如下表:
(1)在如图所示的直角坐标系中以车速为x轴,以刹车距离为y轴描出这些数据所表示的点,并用光滑的曲线连接这些点,得到某函数的大致图象.
(2)观察图象估计函数的类型,并确定一个满足这些数据的函数解析式.
(3)一辆该型号的汽车在国道上发生了交通事故,现场测得刹车距离为46.5米,请推测刹车时速度是多少?请问在事故发生时,汽车是否超速行驶?
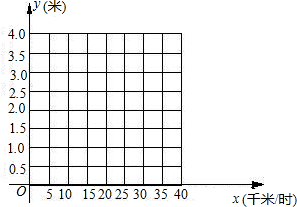
| 刹车时车速(千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 刹车距离(米) | 0 | 0.1 | 0.3 | 0.6 | 1 | 1.5 | 2.1 |
(2)观察图象估计函数的类型,并确定一个满足这些数据的函数解析式.
(3)一辆该型号的汽车在国道上发生了交通事故,现场测得刹车距离为46.5米,请推测刹车时速度是多少?请问在事故发生时,汽车是否超速行驶?

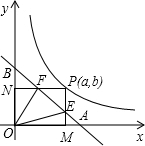 持不变的角?若有,请求出其大小;若没有,请说明理由.
持不变的角?若有,请求出其大小;若没有,请说明理由. ,小华八点离开家,十四点回到家,根据这个曲线图,请回答下列问题:
,小华八点离开家,十四点回到家,根据这个曲线图,请回答下列问题: 相切于点A、B,线段AB=180m,∠ABD=150°。
相切于点A、B,线段AB=180m,∠ABD=150°。 的圆心O;
的圆心O;