题目内容
等边△ABC的边长是3，连接各边中点所成的三角形的周长是（ ）A．9
B．6
C．4.5
D．3
【答案】分析：先根据题意画出图形，首先由三角形的中位线定理得到DF=
BC，DE=
AC，EF=
AB，△DEF的周长是DE+DF+EF，代入即可．
解答：解：
由题意可得，DE、EF、DF都是△ABC的中位线，
故可得DF=
BC，DE=
AC，EF=
AB，
故△DEF的周长=DE+DF+EF=
BC+
AC+
AB=4.5．
故选C．
点评：本题考查了三角形的中位线定理及等边三角形的性质，解答本题的关键是掌握：三角形的中位线平行于第三边，并且等于第三边的一半．
BC，DE=AC，EF=AB，△DEF的周长是DE+DF+EF，代入即可．解答：解：
由题意可得，DE、EF、DF都是△ABC的中位线，
故可得DF=
BC，DE=AC，EF=AB，故△DEF的周长=DE+DF+EF=
BC+AC+AB=4.5．故选C．
点评：本题考查了三角形的中位线定理及等边三角形的性质，解答本题的关键是掌握：三角形的中位线平行于第三边，并且等于第三边的一半．
练习册系列答案
相关题目
等边△ABC的边长为a，顶点A在原点，一条高线恰好落在y轴的负半轴上，则第三象限的顶点B的坐标是（ ）
A、（
| ||||||
B、（-
| ||||||
C、（-
| ||||||
D、（-
|
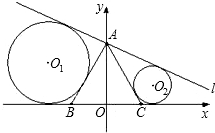交点）．设与AB、l、x轴相切的⊙O1的半径为r1，与AC、l、x轴相切的⊙O2半径为r2
