题目内容
 如图,△OP1A1,△A1P2A2是等腰直角三角形,点P1、P2在函数y=
如图,△OP1A1,△A1P2A2是等腰直角三角形,点P1、P2在函数y=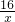 的图象上,斜边OA1、A1A2都在横轴上,则点A2的坐标是________.
的图象上,斜边OA1、A1A2都在横轴上,则点A2的坐标是________.
(8 ,0)
,0)
分析:根据题意,设A1坐标为(a,0),A2为(b,0),则P1坐标为( ,
, ),P2坐标为(
),P2坐标为( ,
,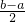 ),然后把P1,P2的坐标依次代入到反比例函数表达式,即可依次求出a、b的值,即可推出结论.
),然后把P1,P2的坐标依次代入到反比例函数表达式,即可依次求出a、b的值,即可推出结论.
解答:设A1坐标为(a,0),A2为(b,0),
∵△OP1A1,△A1P2A2是等腰直角三角形,
∴P1坐标为 ( ,
, ),P2坐标为(
),P2坐标为( ,
,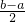 ),
),
∵点P1在函数y=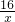 的图象上,
的图象上,
∴ ,
,
∴a1=8,a2=-8(不合题意,舍去),
∴P2坐标为( ,
, )
)
∵点P2在函数y=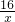 的图象上,
的图象上,
∴ =
= ,
,
∴b1=8 ,b2=-8
,b2=-8 (不合题意,舍去),
(不合题意,舍去),
∴A2为(8 ,0).
,0).
故答案为(8 ,0).
,0).
点评:本题主要考查反比例函数的性质,等腰直角三角形的性质,关键在于设出A1点和A2点的坐标,表示出P1坐标,P2坐标,根据函数表达式求出a、b即可.
 ,0)
,0)分析:根据题意,设A1坐标为(a,0),A2为(b,0),则P1坐标为(
 ,
, ),P2坐标为(
),P2坐标为( ,
,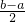 ),然后把P1,P2的坐标依次代入到反比例函数表达式,即可依次求出a、b的值,即可推出结论.
),然后把P1,P2的坐标依次代入到反比例函数表达式,即可依次求出a、b的值,即可推出结论.解答:设A1坐标为(a,0),A2为(b,0),
∵△OP1A1,△A1P2A2是等腰直角三角形,
∴P1坐标为 (
 ,
, ),P2坐标为(
),P2坐标为( ,
,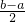 ),
),∵点P1在函数y=
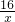 的图象上,
的图象上,∴
 ,
,∴a1=8,a2=-8(不合题意,舍去),
∴P2坐标为(
 ,
, )
)∵点P2在函数y=
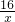 的图象上,
的图象上,∴
 =
= ,
,∴b1=8
 ,b2=-8
,b2=-8 (不合题意,舍去),
(不合题意,舍去),∴A2为(8
 ,0).
,0).故答案为(8
 ,0).
,0).点评:本题主要考查反比例函数的性质,等腰直角三角形的性质,关键在于设出A1点和A2点的坐标,表示出P1坐标,P2坐标,根据函数表达式求出a、b即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,△OP1A1,△A1P2A2是等腰直角三角形,点P1、P2在函数y=
如图,△OP1A1,△A1P2A2是等腰直角三角形,点P1、P2在函数y= 如图,△OP1A1,△A1P2A2,△A2P3A3…都是等腰直角三角形,直角顶点P1,P2,P3…都在函数
如图,△OP1A1,△A1P2A2,△A2P3A3…都是等腰直角三角形,直角顶点P1,P2,P3…都在函数 (x>0)的图象上,若三角形依次排列下去,则A2009的坐标是________.
(x>0)的图象上,若三角形依次排列下去,则A2009的坐标是________. 的图象上,斜边OA1、A1A2都在横轴上,则点A2的坐标是 .
的图象上,斜边OA1、A1A2都在横轴上,则点A2的坐标是 .
 的图象上,斜边OA1、A1A2都在横轴上,则点A2的坐标是 .
的图象上,斜边OA1、A1A2都在横轴上,则点A2的坐标是 .
