题目内容
在直角梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=3 ,CD=7,点P是BC边上的一动点(不与点B重合),过点D作DE⊥AP,垂足为E.
,CD=7,点P是BC边上的一动点(不与点B重合),过点D作DE⊥AP,垂足为E.(1)求AB的长;
(2)设AP=x,DE=y,求y与x之间的函数关系式,并指出自变量x的取值范围;
(3)延长DE交AB于点F,连接PF,当△ADE为等腰直角三角形时,求sin∠FPA的值.

【答案】分析:(1)过D作DG⊥BC,垂足为G,已知CD=7及∠C=45°,根据三角函数可求得AB的长.
(2)已知∠B=∠AED=90°,AD∥BC,得到∠DAE=∠APB,根据有两组角相等的两个三角形相似得到△ABP∽△DEA,从而得到对应边成比例即 ,从而可得到自变量x的取值范围.
,从而可得到自变量x的取值范围.
(3)根据题意可得到AE=DE=EF,从而可求得AP、PE,根据勾股定理求得PF的长,此时再求sin∠FPA的值就不难了.
解答: 解:(1)过D作DG⊥BC,垂足为G.(1分)
解:(1)过D作DG⊥BC,垂足为G.(1分)
AB=DG=CDsinC=7× .(3分)
.(3分)
(2)∵∠B=∠AED=90°,AD∥BC
∴∠DAE=∠APB
∴△ABP∽△DEA(4分)
∴ ,
, ,
, .(5分)
.(5分)
取值范围是 .(6分)
.(6分)
(3)由题意知:AE=DE=EF=ADsin45°=3 =3.(7分)
=3.(7分)
∴AP= =7,PE=7-3=4.(8分)
=7,PE=7-3=4.(8分)
PF= ,(9分)
,(9分)
∴sin∠FPA= .(10分)
.(10分)
点评:此题主要考查学生对相似三角形的判定及解直角三角形的理解及运用.
(2)已知∠B=∠AED=90°,AD∥BC,得到∠DAE=∠APB,根据有两组角相等的两个三角形相似得到△ABP∽△DEA,从而得到对应边成比例即
 ,从而可得到自变量x的取值范围.
,从而可得到自变量x的取值范围.(3)根据题意可得到AE=DE=EF,从而可求得AP、PE,根据勾股定理求得PF的长,此时再求sin∠FPA的值就不难了.
解答:
 解:(1)过D作DG⊥BC,垂足为G.(1分)
解:(1)过D作DG⊥BC,垂足为G.(1分)AB=DG=CDsinC=7×
 .(3分)
.(3分)(2)∵∠B=∠AED=90°,AD∥BC
∴∠DAE=∠APB
∴△ABP∽△DEA(4分)
∴
 ,
, ,
, .(5分)
.(5分)取值范围是
 .(6分)
.(6分)(3)由题意知:AE=DE=EF=ADsin45°=3
 =3.(7分)
=3.(7分)∴AP=
 =7,PE=7-3=4.(8分)
=7,PE=7-3=4.(8分)PF=
 ,(9分)
,(9分)∴sin∠FPA=
 .(10分)
.(10分)点评:此题主要考查学生对相似三角形的判定及解直角三角形的理解及运用.

练习册系列答案
相关题目
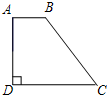 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
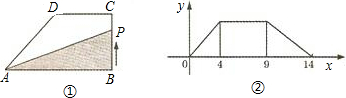
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )