题目内容
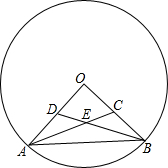（2013•香坊区三模）如图，OA、OB为⊙O的半径，OA⊥OB，连接AB，点C、D分别为OB、OA的中点，线段AC、BD相交于E（1）求证：AC=BD；
（2）若BE=2
| 5 |
分析：（1）求出OC=OD，根据SAS证出△AOC≌△BOD即可．
（2）连接DC，根据三角形中位线求出△DCE∽△BAE，得出比例式，求出DE，求出DB，根据勾股定理求出OD，即可得出答案．
（2）连接DC，根据三角形中位线求出△DCE∽△BAE，得出比例式，求出DE，求出DB，根据勾股定理求出OD，即可得出答案．
解答：解：（1）∵OA=OB，点C、D分别为OB、OA的中点，
∴OC=OD，
在△AOC和△BOD中，
，
∴△AOC≌△BOD，
∴AC=BD．
（2）连接DC，
∵点C、D分别为OB、OA的中点，
∴DC∥AB，
∴∠DCA=∠CAB，∠DEC=∠AEB，
∴△DCE∽△BAE，
∴
=
=
，
∴DE=
BE=
，
∴DB=3
，
在Rt△OBD中，OD2+（2OD）2=BD2，
∴OD=3，
∴BO=AO=2OD=6．
∴OC=OD，
在△AOC和△BOD中，
|
∴△AOC≌△BOD，
∴AC=BD．
（2）连接DC，
∵点C、D分别为OB、OA的中点，
∴DC∥AB，
∴∠DCA=∠CAB，∠DEC=∠AEB，
∴△DCE∽△BAE，
∴
| DC |
| AB |
| DE |
| BE |
| 1 |
| 2 |
∴DE=
| 1 |
| 2 |
| 5 |
∴DB=3
| 5 |
在Rt△OBD中，OD2+（2OD）2=BD2，
∴OD=3，
∴BO=AO=2OD=6．
点评：本题考查了相似三角形的性质和判定，三角形中位线，勾股定理，全等三角形的性质和判定的应用，主要考查学生运用定理进行推理和计算的能力．
练习册系列答案
相关题目