Question

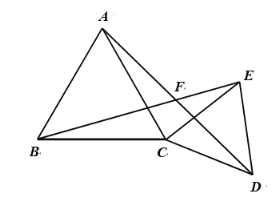
【题目】如图，AD，BC相交于点O，AC=BD，∠C =∠D=90°．

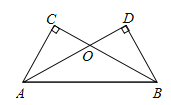
（1）求证：OA=OB；

（2）若∠ABC=30°，OC=5，求BC的长．

Answer 1

【答案】（1）见解析；（2）15

【解析】

(1)用HL证明Rt△ABC和Rt△BAD全等，然后用全等三角形的性质即可证明；

（1）先说明∠ABC=∠DAB=30°，再得到∠AOC=60°，再求得∠OAC=30°，可得AO=2OC,最后根据线段的和差即可解答.

（1）证明：在Rt△ABC和Rt△BAD中，

∴Rt△ABC≌Rt△BAD（HL）

∴∠ABC=∠DAB．

∴OA=OB．

（2）∵∠ABC=30°，

∴∠ABC=∠DAB=30°．

∴∠AOC=∠ABC+∠DAB=30°+30°=60°．

在Rt△AOC中，

∴∠OAC=90°－60°=30°．

∴OA=2OC=5×2=10．

∴OB=OA=10．

∴BC=OB+OC=5+10=15