Question

【题目】如图，在四边形ABCD中，AB=，AD=7，BC=8，tan∠B=，∠C=∠D，则线段CD的长为_____．

Answer 1

【答案】

【解析】

作AH⊥BC于H，在CB上截取CE，使得CE＝AD，连接AE，作DM⊥AE于M，CN⊥AE于N．构造等腰梯形，把等腰梯形分成两个全等三角形一个矩形解决问题即可．

如图，作AH⊥BC于H，在CB上截取CE，使得CE＝AD，连接AE，作DM⊥AE于M，CN⊥AE于N，

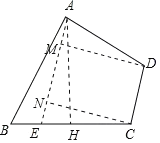
∵∠ADC＝∠ECD，DA＝CE，

∴四边形ADCE是等腰梯形，则△ADM≌△ECN，可得AM＝EN，四边形MNCD是矩形，可得CD＝MN，

在Rt△ABH中，∵tanB＝，AB＝，

∴AH＝5，BH＝2，

∵BC＝8，EC＝AD＝7，

∴BE＝87＝1，

∴EH＝BHBE＝1，

在Rt△AEH中，AE＝＝，

∵△ECN∽△EAH，

∴，

∴EN＝，

∴AM＝EN＝，

∴CD＝MN＝AEAMEN＝，

故答案为：．