Ő‚ńŅńŕ»›
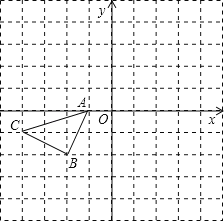
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy=![]() x2+bx+c”Žx÷ŠĹĽ”ŕĶ„A£®©Ā2£¨0£©£¨ĹĽy÷Š”ŕĶ„B£®0£¨
x2+bx+c”Žx÷ŠĹĽ”ŕĶ„A£®©Ā2£¨0£©£¨ĹĽy÷Š”ŕĶ„B£®0£¨![]() £©£ģ÷ĪŌŖy=kx
£©£ģ÷ĪŌŖy=kx![]() ĻżĶ„A”Žy÷ŠĹĽ”ŕĶ„C£¨”ŽŇ◊őÔŌŖĶńŃŪ“ĽłŲĹĽĶ„ «D£ģ
ĻżĶ„A”Žy÷ŠĹĽ”ŕĶ„C£¨”ŽŇ◊őÔŌŖĶńŃŪ“ĽłŲĹĽĶ„ «D£ģ
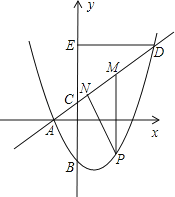
£®1£©«ůŇ◊őÔŌŖy=![]() x2+bx+c”Ž÷ĪŌŖy=kx
x2+bx+c”Ž÷ĪŌŖy=kx![]() ĶńĹ‚őŲ Ĺ£Ľ
ĶńĹ‚őŲ Ĺ£Ľ
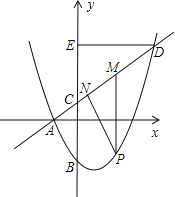
£®2£©…ŤĶ„P «÷ĪŌŖADŌ¬∑ĹĶńŇ◊őÔŌŖ…Ō“Ľ∂ĮĶ„£®≤Ľ”ŽĶ„A°ĘD÷ōļŌ£©£¨ĻżĶ„P◊ųy÷ŠĶń∆Ĺ––ŌŖ£¨ĹĽ÷ĪŌŖAD”ŕĶ„M£¨◊ųDE°Õy÷Š”ŕĶ„E£ģŐĹĺŅ£ļ «∑Ůīś‘ŕ’‚—ýĶńĶ„P£¨ ĻňńĪŖ–őPMEC «∆Ĺ––ňńĪŖ–ő£Ņ»Űīś‘ŕ«Ž«ů≥ŲĶ„PĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨◊ųPN°ÕAD”ŕĶ„N£¨…Ť°ųPMNĶń÷‹≥§ő™m£¨Ķ„PĶńļŠ◊ÝĪÍő™x£¨«ům”ŽxĶńļĮ żĻōŌĶ Ĺ£¨≤Ę«ů≥ŲmĶń◊Óīů÷Ķ£ģ
°ĺīūįł°Ņ£®1£©y=![]() x2©Ā
x2©Ā![]() x©Ā
x©Ā![]() £¨y=
£¨y=![]() x+
x+![]() £Ľ£®2£©PĶń◊ÝĪÍ «£®2£¨©Ā3£©ļÕ£®4£¨©Ā
£Ľ£®2£©PĶń◊ÝĪÍ «£®2£¨©Ā3£©ļÕ£®4£¨©Ā![]() £©£ĽņŪ”…ľŻĹ‚őŲ£Ľ£®3£©ĶĪx=3 Ī£¨mĶń◊Óīů÷Ķ «15£¨
£©£ĽņŪ”…ľŻĹ‚őŲ£Ľ£®3£©ĶĪx=3 Ī£¨mĶń◊Óīů÷Ķ «15£¨
°ĺĹ‚őŲ°Ņ
‘Ő‚∑÷őŲ£ļ£®1£©į—Ķ„A°ĘBĶń◊ÝĪÍ∑÷Īūīķ»ŽŇ◊őÔŌŖĹ‚őŲ Ĺ£¨Ń–≥ŲĻō”ŕb°ĘcĶń∑Ĺ≥Ő◊ť£¨Õ®ĻżĹ‚∑Ĺ≥Ő◊ťŅ…“‘«ůĶ√b°ĘcĶń÷Ķ£Ľį—Ķ„AĶń◊ÝĪÍīķ»Ž“ĽīőļĮ żĹ‚őŲ Ĺ£¨Ń–≥ŲĻō”ŕkĶń∑Ĺ≥Ő£¨Õ®ĻżĹ‚∑Ĺ≥Ő«ůĶ√kĶń÷Ķ£Ľ
£®2£©łýĺ›∆Ĺ––ňńĪŖ–őĶń–‘÷ Õ∆÷™EC=PM£ģ“◊«ůĶ„DĶń◊ÝĪÍ «£®8£¨7![]() £©£¨Ķ„CĶń◊ÝĪÍ «£®0£¨
£©£¨Ķ„CĶń◊ÝĪÍ «£®0£¨![]() £©£¨‘ÚCE=6£ģ…ŤPĶń◊ÝĪÍ «£®x£¨
£©£¨‘ÚCE=6£ģ…ŤPĶń◊ÝĪÍ «£®x£¨![]() x2©Ā
x2©Ā![]() x©Ā
x©Ā![]() £©£¨‘ÚMĶń◊ÝĪÍ «£®x£¨
£©£¨‘ÚMĶń◊ÝĪÍ «£®x£¨![]() x+
x+![]() £©£¨
£©£¨
‘ÚPM=£®![]() x+
x+![]() £©©Ā£®
£©©Ā£®![]() x2©Ā
x2©Ā![]() x©Ā
x©Ā![]() £©=©Ā
£©=©Ā![]() x2+
x2+![]() x+4£¨ňý“‘”…EC=PMĶ√ĶĹ©Ā
x+4£¨ňý“‘”…EC=PMĶ√ĶĹ©Ā![]() x2+
x2+![]() x+4=6£¨Õ®ĻżĹ‚∑Ĺ≥Ő«ůĶ√Ķ„PĶń◊ÝĪÍ «£®2£¨©Ā3£©ļÕ£®4£¨©Ā
x+4=6£¨Õ®ĻżĹ‚∑Ĺ≥Ő«ůĶ√Ķ„PĶń◊ÝĪÍ «£®2£¨©Ā3£©ļÕ£®4£¨©Ā![]() £©£Ľ
£©£Ľ
£®3£©Õ®ĻżŌŗň∆»żĹ«–ő°ųPMN°◊°ųCDEĶń–‘÷ Õ∆÷™£ļ![]() =
=![]() £¨į—ŌŗĻō żĺ›īķ»Ž≤Ę’ŻņŪŅ…“‘Ķ√≥Ųm”ŽxĶńļĮ żĻōŌĶ Ĺ «£ļm=©Ā
£¨į—ŌŗĻō żĺ›īķ»Ž≤Ę’ŻņŪŅ…“‘Ķ√≥Ųm”ŽxĶńļĮ żĻōŌĶ Ĺ «£ļm=©Ā![]() x2+
x2+![]() x+
x+![]() =©Ā
=©Ā![]() £®x©Ā3£©2+15£¨
£®x©Ā3£©2+15£¨
”…Ň◊őÔŌŖĶń–‘÷ Ņ…“‘Ķ√ĶĹ£ļm”–◊Óīů÷Ķ£¨ĶĪx=3 Ī£¨mĶń◊Óīů÷Ķ «15£ģ
Ĺ‚£ļ£®1£©°Ŗy=![]() x2+bx+cĺ≠ĻżĶ„A£®©Ā2£¨0£©ļÕB£®0£¨
x2+bx+cĺ≠ĻżĶ„A£®©Ā2£¨0£©ļÕB£®0£¨![]() £©
£©
°ŗ”…īňĶ√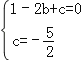 £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√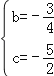
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺ «y=![]() x2©Ā
x2©Ā![]() x©Ā
x©Ā![]() £Ľ
£Ľ
°Ŗ÷ĪŌŖy=kx![]() ĺ≠ĻżĶ„A£®©Ā2£¨0£©
ĺ≠ĻżĶ„A£®©Ā2£¨0£©
°ŗ©Ā2k+![]() =0£¨
=0£¨
Ĺ‚Ķ√£ļk=![]() £¨
£¨
°ŗ÷ĪŌŖĶńĹ‚őŲ Ĺ « y=![]() x+
x+![]() £Ľ
£Ľ
£®2£©Ņ…«ůDĶń◊ÝĪÍ «£®8£¨7![]() £©£¨Ķ„CĶń◊ÝĪÍ «£®0£¨
£©£¨Ķ„CĶń◊ÝĪÍ «£®0£¨![]() £©£¨
£©£¨
°ŗCE=6£¨
…ŤPĶń◊ÝĪÍ «£®x£¨![]() x2©Ā
x2©Ā![]() x©Ā
x©Ā![]() £©£¨‘ÚMĶń◊ÝĪÍ «£®x£¨
£©£¨‘ÚMĶń◊ÝĪÍ «£®x£¨![]() x+
x+![]() £©
£©
“Úő™Ķ„P‘ŕ÷ĪŌŖADĶńŌ¬∑Ĺ£¨
īň ĪPM=£®![]() x+
x+![]() £©©Ā£®
£©©Ā£®![]() x2©Ā
x2©Ā![]() x©Ā
x©Ā![]() £©=©Ā
£©=©Ā![]() x2+
x2+![]() x+4£¨
x+4£¨
”…”ŕPM°őy÷Š£¨“™ ĻňńĪŖ–őPMEC «∆Ĺ––ňńĪŖ–ő£¨Īō”–PM=CE£¨
ľī©Ā![]() x2+
x2+![]() x+4=6
x+4=6
Ĺ‚’‚łŲ∑Ĺ≥ŐĶ√£ļx1=2£¨x2=4£¨
ĶĪx=2 Ī£¨y=©Ā3£¨
ĶĪx=4 Ī£¨y=©Ā![]() £¨
£¨
“Úīň£¨÷ĪŌŖADŌ¬∑ĹĶńŇ◊őÔŌŖ…Ōīś‘ŕ’‚—ýĶńĶ„P£¨ ĻňńĪŖ–őPMEC «∆Ĺ––ňńĪŖ–ő£¨
Ķ„PĶń◊ÝĪÍ «£®2£¨©Ā3£©ļÕ£®4£¨©Ā![]() £©£Ľ
£©£Ľ
£®3£©‘ŕRt°ųCDE÷–£¨DE=8£¨CE=6 ”…ĻīĻ…∂®ņŪĶ√£ļDC=![]() =10
=10
°ŗ°ųCDEĶń÷‹≥§ «24£¨
°ŖPM°őy÷Š£¨°ŗ°ŌPMN=°ŌDCE£¨
°Ŗ°ŌPNM=°ŌDEC=90°„£¨°ŗ°ųPMN°◊°ųCDE£¨
°ŗ![]() =
=![]() £¨ľī
£¨ľī ![]() =
=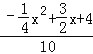 £¨
£¨
ĽĮľÚ’ŻņŪĶ√£ļm”ŽxĶńļĮ żĻōŌĶ Ĺ «£ļm=©Ā![]() x2+
x2+![]() x+
x+![]() £¨
£¨
m=©Ā![]() x2+
x2+![]() x+
x+![]() =©Ā
=©Ā![]() £®x©Ā3£©2+15£¨
£®x©Ā3£©2+15£¨
°Ŗ©Ā![]() £ľ0£¨
£ľ0£¨
°ŗm”–◊Óīů÷Ķ£¨ĶĪx=3 Ī£¨mĶń◊Óīů÷Ķ «15£ģ

 ĹÚ«ŇĹŐ”żľ∆ň„–°◊ī‘™ŌĶŃ–īūįł
ĹÚ«ŇĹŐ”żľ∆ň„–°◊ī‘™ŌĶŃ–īūįł