题目内容
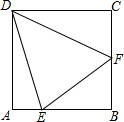 在正方形ABCD中,E是AB上一点,F是BC上一点,且EF=AE+CF,则∠EDF度数为
在正方形ABCD中,E是AB上一点,F是BC上一点,且EF=AE+CF,则∠EDF度数为
- A.30°
- B.60°
- C.45°
- D.小于60°
C
分析:根据正方形的性质得到DA=DC,∠DAB=∠C=90°,则可把△DCF绕点D顺时针旋转90°得到△DAG,根据旋转的性质得到∠DAG=∠C=90°,GA=CF,∠GAF=90°,DG=DF,于是得点G在BA的延长线上,易得GE=EF,易证得△DGE≌△DFE,则∠GDE=∠FDE,所以∠EDF= ∠GDF=45°.
∠GDF=45°.
解答:∵四边形ABCD为正方形,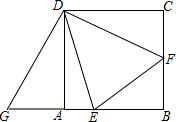
∴DA=DC,∠DAB=∠C=90°,
∴把△DCF绕点D顺时针旋转90°得到△DAG,如图,
∴∠DAG=∠C=90°,GA=CF,∠GAF=90°,DG=DF,
∴点G在BA的延长线上,
∴GE=GA+AE,
∵EF=AE+CF,
∴GE=EF,
在△DGE和△DFE中
 ,
,
∴△DGE≌△DFE,
∴∠GDE=∠FDE,
∴∠EDF= ∠GDF=45°.
∠GDF=45°.
故选C.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正方形的性质以及全等三角形的判定与性质.
分析:根据正方形的性质得到DA=DC,∠DAB=∠C=90°,则可把△DCF绕点D顺时针旋转90°得到△DAG,根据旋转的性质得到∠DAG=∠C=90°,GA=CF,∠GAF=90°,DG=DF,于是得点G在BA的延长线上,易得GE=EF,易证得△DGE≌△DFE,则∠GDE=∠FDE,所以∠EDF=
 ∠GDF=45°.
∠GDF=45°.解答:∵四边形ABCD为正方形,

∴DA=DC,∠DAB=∠C=90°,
∴把△DCF绕点D顺时针旋转90°得到△DAG,如图,
∴∠DAG=∠C=90°,GA=CF,∠GAF=90°,DG=DF,
∴点G在BA的延长线上,
∴GE=GA+AE,
∵EF=AE+CF,
∴GE=EF,
在△DGE和△DFE中
 ,
,∴△DGE≌△DFE,
∴∠GDE=∠FDE,
∴∠EDF=
 ∠GDF=45°.
∠GDF=45°.故选C.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正方形的性质以及全等三角形的判定与性质.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF=
已知:如图所示,在正方形ABCD中,E为AD的中点,F为DC上的一点,且DF= 18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
 如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.
如图,在正方形ABCD中,P是CD上一点,且AP=BC+CP,Q为CD中点,求证:∠BAP=2∠QAD.