题目内容

精英家教网正方形纸片ABCD和BEFG的边长分别为5和2，按如图所示的方式剪下2个阴影部分的直角三角形，并摆放成正方形DHFI，则正方形DHFI的边长为
 
．
分析：根据已知可求得正方形DHFI面积，再根据面积公式即可求得其边长．
解答：解：根据图可得正方形DHFI面积=正方形纸片ABCD和BEFG的面积之和=52+22=29，
那么就可求得正方形DHFI的边长=
29
．
故答案为
29
．
点评：解决本题的关键是得到所求正方形的面积和已知正方形面积之间的关系．
练习册系列答案
相关题目
（2011•鄞州区模拟）在一次研究性学习活动中，某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住，保持正方形ABCD不动，顺时针旋转正方形EFGH，如图所示．
（1）小组成员经观察、测量，发现在旋转过程中，有许多有趣的结论．下面是旋转角度小于90°时他们得到的一些猜想：
①ME=MA
②两张正方形纸片的重叠部分的面积为定值；
③∠MON保持45°不变．
请你对这三个猜想做出判断（正确的在序号后的括号内打上“√”，错误的打上“×”）：
①
√
√
  ②
×
×
 ③
√
√

（2）上面的三个猜想中若有正确的，请选择其中的一个给予证明；若都是错误的，请选择其一说明理由．
（3）小组成员还发现：（1）中的△ENN的面积S随着旋转角度∠AOE的变化而变化．请你指出当旋转角∠AOE为多少度时△ENN的面积S取得最大值．（不必证明）
在一次研究性学习活动中，某小组将两张互相重合的正方形纸片ABCD和EFGH的中心O用图钉固定住，保持正方形ABCD不动，顺时针旋转正方形EFGH，如图所示．小组成员经观察、测量，发现在旋转过程中，有许多有趣的结论．下面是旋转角度小于90°时他们得到的一些猜想：
①ME=MA；
②两张正方形纸片的重叠部分的面积为定值；
③∠MON保持45°不变；
④△EMN的面积S随着旋转角度∠AOE的变化而变化．当旋转角∠AOE为45°时△ENN的面积S取得最大值．
请你对这四个猜想作出判断，把正确的猜想序号写在横线上
①③④
①③④
．
图1是两个正方形纸片ABCD和CEFG叠放在一起，分别以BC边所在直线和BC边的中垂线为坐标轴建立如图所示的坐标系，其中B（-2，0），E（2，
2
），C（2，0），固定正方形ABCD，直线L经过AC两点；将正方形CEFG绕点C顺时针旋转135°得到正方形CE1F1G1，
（1）在图2中求点E1的坐标，并直接写出点E1与直线L的位置关系．
（2）利用（1）的结论，将图2中的正方形CE1F1G1在射线CA上沿着CA方向以每秒1个单位的速度平移，平移后的正方形CE1F1G1设为正方形PQRH（图3），当点R移动到点A停止，设正方形PQRH移动的时间为t秒，正方形PQRH与正方形ABCD重叠部分的面积为S，请直接写出S与t之间的函数解析式，并写出函数自变量t的取值范围．
（3）在（2）的条件下，如果S=1时，过BP的直线为m，M点为直线m上的动点，N为直线L上的动点，那么是否存在平行四边形MNBC，如果存在，请求出M点的坐标，如果不存在，请说明理由．
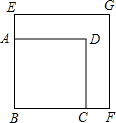如图，将两个正方形纸片ABCD和EBFG重叠，且使直角B完全重合，然后用剪刀将它剪成若干小纸片，恰能拼成一个大正方形．请用两次剪断（按直线剪断算一次）完成此项任务，用虚线在图上画出剪痕．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网