题目内容
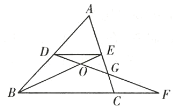
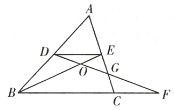
【题目】如图,在![]() 中,点
中,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,
的中点,![]() 过
过![]() 的中点
的中点![]() 并与
并与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() 的面积为
的面积为![]() ,则四边形
,则四边形![]() 的面积=______.
的面积=______.
【答案】![]()
【解析】
由点D、E分别是边AB、AC的中点,可得DE∥BC,DE=![]() BC,即可得△ADE∽△ABC与△ODE∽△OFB,又由EC的中点是G,则可得△DEG≌△FCG,然后由相似三角形的面积比等于相似比的平方与等高三角形的面积比等于对应底的比即可求得答案.
BC,即可得△ADE∽△ABC与△ODE∽△OFB,又由EC的中点是G,则可得△DEG≌△FCG,然后由相似三角形的面积比等于相似比的平方与等高三角形的面积比等于对应底的比即可求得答案.
解:∵点D、E分别是边AB、AC的中点,
![]()
![]()
![]()
∵△ADE的面积为S,
∴S△ABC=4S,
∵DE∥BC,
∴△ODE∽△OFB,∠EDG=∠F,∠DEG=∠GCF,
![]()
又EG=CG,
∴△DEG≌△FCG(AAS),
∴DE=CF,
∴BF=3DE,
∵DE∥BC,
∴△ODE∽△OFB
![]()
∵AD=BD,
∴S△BDE=S△ADE=S,
∵AE=CE=2EG,
![]()
![]()
![]()
![]()
∵S四边形DBCE=S△ABC-S△ADE=3S,
∴S四边形OBCG=S四边形DBCE-S△BDE-S△OEG=3S-S-![]()
故答案为:![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目