题目内容
已知:关于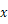 的方程
的方程
(1)当 取何值时,二次函数
取何值时,二次函数 的对称轴是直线
的对称轴是直线 ;
;
(2)求证: 取任何实数时,方程
取任何实数时,方程 总有实数根.
总有实数根.
(1)解:∵ 二次函数的对称轴是直线,
∴,解得
经检验是原方程的解.
故时,二次函数的对称轴是直线.
(2)证明:①当时,原方程变为,方程的解为;
②当时,原方程为一元二次方程,,
当∆方程总有实数根,∴
整理,得 即
∵ 时,总成立.
∴ 取任何实数时,方程总有实数根.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
已知:关于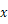 的方程
的方程
(1)当 取何值时,二次函数
取何值时,二次函数 的对称轴是直线
的对称轴是直线 ;
;
(2)求证: 取任何实数时,方程
取任何实数时,方程 总有实数根.
总有实数根.
(1)解:∵ 二次函数的对称轴是直线,
∴,解得
经检验是原方程的解.
故时,二次函数的对称轴是直线.
(2)证明:①当时,原方程变为,方程的解为;
②当时,原方程为一元二次方程,,
当∆方程总有实数根,∴
整理,得 即
∵ 时,总成立.
∴ 取任何实数时,方程总有实数根.

 名校课堂系列答案
名校课堂系列答案