题目内容
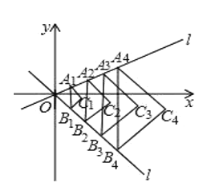
【题目】如图，在平面直角坐标系中，
、
、
、…、
均为等腰直角三角形，且
，点
、
、
、……、
和点
、
、
、……、
分别在正比例函数
和
的图象上，且点、、、……、的横坐标分别为1，2，3…
，线段
、
、
、…、
均与
轴平行.按照图中所反映的规律，则的顶点
的坐标是_____．（其中为正整数）
【答案】
【解析】
当x=1代入
和 
中，求出A1，B1的坐标，再由△A1B1C1为等腰直角三角形，求出C1的坐标，同理求出C2，C3，C4的坐标，找到规律，即可求出
的顶点
的坐标.
当x=1代入和中，得：
，
，
∴
，
，
∴
，
∵△A1B1C1为等腰直角三角形，
∴C1的横坐标为
，
C1的纵坐标为
，
∴C1的坐标为
；
当x=2代入和中，得：
，
，
∴
，
，
∴
，
∵△A2B2C2为等腰直角三角形，
∴C2的横坐标为
，
C2的纵坐标为
，
∴C2的坐标为
；
同理，可得C3的坐标为
；C4的坐标为
；
∴的顶点的坐标是，
故答案为：.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
