题目内容
 如图,反比例函数y1=
如图,反比例函数y1= 和y2=
和y2= 的图象如图所示,点A为y2=
的图象如图所示,点A为y2= 图象上的任意一点,过A作AC⊥X轴于C,交y1=
图象上的任意一点,过A作AC⊥X轴于C,交y1= 的图象于N;作AB⊥y轴于B,交y1=
的图象于N;作AB⊥y轴于B,交y1= 的图象于M,如有下三个判断:
的图象于M,如有下三个判断:
①S△OCN=S△OBM;②S△四边形ONAM=k-1;③AM=AN.
其中正确的有________(填番号)
①②
分析:利用反比例函数的性质得出M,N的横纵坐标乘积xy=1,以及A在y2= 的图象上,即可得出xy=k,进而求出S△OCN=S△OBM;S△四边形ONAM=k-1.
的图象上,即可得出xy=k,进而求出S△OCN=S△OBM;S△四边形ONAM=k-1.
解答:①∵点M,N在反比例函数y1= 图象上,
图象上,
∴M,N的横纵坐标乘积等于xy=1,
∴S△OCN=S△OBM= ,故此选项正确;
,故此选项正确;
②∵A在y2= 的图象上,
的图象上,
∴xy=k,
∴S△四边形ONAM=k,
∵S△OCN=S△OBM= ,
,
∴S△四边形ONAM=k-1;故此选项正确;
③∵BM×BO=CN×CO,BO不一定等于CO,
∴BM不一定等于CN,
∴无法确定AM是否等于AN,故此选项错误.
故答案为:①②.
点评:此题主要考查了反比例函数的性质,解题的关键是根据已知得出S△四边形ONAM=k,S△OCN=S△OBM= .
.
分析:利用反比例函数的性质得出M,N的横纵坐标乘积xy=1,以及A在y2=
 的图象上,即可得出xy=k,进而求出S△OCN=S△OBM;S△四边形ONAM=k-1.
的图象上,即可得出xy=k,进而求出S△OCN=S△OBM;S△四边形ONAM=k-1.解答:①∵点M,N在反比例函数y1=
 图象上,
图象上,∴M,N的横纵坐标乘积等于xy=1,
∴S△OCN=S△OBM=
 ,故此选项正确;
,故此选项正确;②∵A在y2=
 的图象上,
的图象上,∴xy=k,
∴S△四边形ONAM=k,
∵S△OCN=S△OBM=
 ,
,∴S△四边形ONAM=k-1;故此选项正确;
③∵BM×BO=CN×CO,BO不一定等于CO,
∴BM不一定等于CN,
∴无法确定AM是否等于AN,故此选项错误.
故答案为:①②.
点评:此题主要考查了反比例函数的性质,解题的关键是根据已知得出S△四边形ONAM=k,S△OCN=S△OBM=
 .
. 
练习册系列答案
相关题目
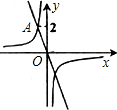 如图,反比例函数y1=
如图,反比例函数y1=| k |
| x |
| A、-2<X<2 |
| B、-1<x<0或x>1 |
| C、x<-1或0<x<1 |
| D、x<-1或x>1 |
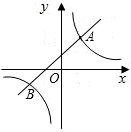 如图,反比例函数
如图,反比例函数 (2012•滦南县一模)如图,反比例函数
(2012•滦南县一模)如图,反比例函数 已知如图:反比例函数
已知如图:反比例函数 如图,反比例函数y1=
如图,反比例函数y1=