题目内容
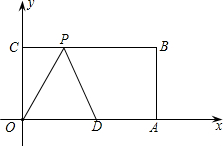已知：如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（6，0），C（0，2），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为3的等腰三角形时，点P的坐标是分析：有两种情况：①当OP=OD=3时，由勾股定理求出OP，即可求出答案；②当PD=OD=3时，过D作DE⊥OB于E，由勾股定理求出PE，即可求出P的坐标．
解答：
解：∵OD=3，OC=2，
有两种情况：①当OP=OD=3时，由勾股定理得：OP=
=
，
∴P（
，2）；
②当PD=OD=3时，过D作DE⊥OB于E，由勾股定理得：PE=
，
∴P（3-
，2）和P（3+
，2）．
故答案为：（
，2）和（3-
，2）和P（3+
，2）．
解：∵OD=3，OC=2，有两种情况：①当OP=OD=3时，由勾股定理得：OP=
| OP2-OD2 |
| 5 |
∴P（
| 5 |
②当PD=OD=3时，过D作DE⊥OB于E，由勾股定理得：PE=
| 5 |
∴P（3-
| 5 |
| 5 |
故答案为：（
| 5 |
| 5 |
| 5 |
点评：本题主要考查对矩形的性质，坐标与图形性质，勾股定理，等腰三角形的性质等知识点的理解和掌握，能求出所有情况的P的坐标是解此题的关键．
练习册系列答案
相关题目
如图，在平面直角坐标系中，直
如图，在平面直角坐标系中，原点O处有一乒乓球发射器向空中发射乒乓球，乒乓球飞行路线是一条抛物线，在地面上落点落在X轴上为点B．有人在线段OB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让乒乓球落入桶内．已知OB=4米，OC=3米，乒乓球飞行最大高度MN=5米，圆柱形桶的直径为0.5，高为0.3米（乒乓球的体积和圆柱形桶的厚度忽略不计）．
