题目内容
(1)如图1,四边形ACDG与四边形ECBH都是正方形,且B,C,D在一条直线上,连接DE并延长交线段AB于点F.求证:AB=DE,AB⊥DE;
(2)如果将(1)中的两个正方形换成两个矩形,如图2,且
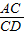 =
=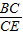 =
=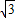 ,则AB与DE的数量关系与位置关系会发生什么变化?请说明你的看法和理由.
,则AB与DE的数量关系与位置关系会发生什么变化?请说明你的看法和理由.(3)如果将(1)中的两个正方形换成两个直角三角形,如图3,∠BCE=∠ACD=90°,且
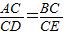 =k,且请直接写出AB与DE的数量关系与位置关系.
=k,且请直接写出AB与DE的数量关系与位置关系.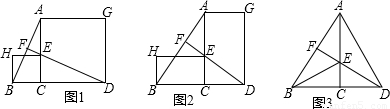
【答案】分析:(1)证明△ABC≌△DEC,则可以得到AB=DE,然后证明∠EDC+∠ABC=90°,则依据三角形内角和定理证得:∠BFD=90°,证得AB⊥DE;
(2)利用相似三角形的判定得出△ABC∽△DEC,根据相似三角形的边的比相等证得AB、DE的关系,与(1)的方法相同证得AB⊥DE;
(3)利用相似三角形的判定得出△ABC∽△DEC,与(2)的方法相同,即可求得.
解答:证明:(1)在△ABC和△DEC中,
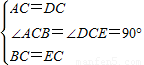 ,
,
∴△ABC≌△DEC(SAS).
∴AB=DE,∠BAC=∠EDC.
∵∠BAC+∠ABC=90°,
∴∠EDC+∠ABC=90°.
∴∠BFD=90°.
∴AB⊥DE.
(2)AB=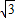 DE,AB⊥DE.
DE,AB⊥DE.
∵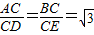 ,∠ACB=∠DCE=90°,
,∠ACB=∠DCE=90°,
∴△ABC∽△DEC.
∴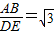 ,∠BAC=∠EDC.
,∠BAC=∠EDC.
∵∠BAC+∠ABC=90°,
∴∠EDC+∠ABC=90°.
∴∠BFD=90°.
∴AB⊥DE.
(3)∵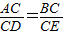 =k,∠ACB=∠ACD
=k,∠ACB=∠ACD
∴△ABC∽△DEC,
∴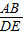 =
=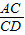 =k,∠BAC=∠CDE,
=k,∠BAC=∠CDE,
又∵∠AEF=∠CED,AC⊥CD,
∴∠BAC+∠AEF=∠DEC+∠CDE=90°
∴∠AFE=90°,
∴AB⊥DE
点评:本题考查了全等三角形的判定与性质,相似三角形的判定与性质,理解相似与全等的关系,理解每个小题之间的联系是关键.
(2)利用相似三角形的判定得出△ABC∽△DEC,根据相似三角形的边的比相等证得AB、DE的关系,与(1)的方法相同证得AB⊥DE;
(3)利用相似三角形的判定得出△ABC∽△DEC,与(2)的方法相同,即可求得.
解答:证明:(1)在△ABC和△DEC中,
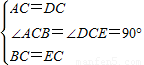 ,
,∴△ABC≌△DEC(SAS).
∴AB=DE,∠BAC=∠EDC.
∵∠BAC+∠ABC=90°,
∴∠EDC+∠ABC=90°.
∴∠BFD=90°.
∴AB⊥DE.
(2)AB=
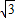 DE,AB⊥DE.
DE,AB⊥DE. ∵
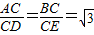 ,∠ACB=∠DCE=90°,
,∠ACB=∠DCE=90°,∴△ABC∽△DEC.
∴
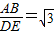 ,∠BAC=∠EDC.
,∠BAC=∠EDC.∵∠BAC+∠ABC=90°,
∴∠EDC+∠ABC=90°.
∴∠BFD=90°.
∴AB⊥DE.
(3)∵
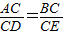 =k,∠ACB=∠ACD
=k,∠ACB=∠ACD∴△ABC∽△DEC,
∴
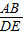 =
=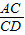 =k,∠BAC=∠CDE,
=k,∠BAC=∠CDE,又∵∠AEF=∠CED,AC⊥CD,
∴∠BAC+∠AEF=∠DEC+∠CDE=90°
∴∠AFE=90°,
∴AB⊥DE
点评:本题考查了全等三角形的判定与性质,相似三角形的判定与性质,理解相似与全等的关系,理解每个小题之间的联系是关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论: 如图,平行四边形ABCD的对角线AC与BD相交于点O,点E、F在对角线AC上,且AF=CE.试问BE∥FD吗?说说你的理由.
如图,平行四边形ABCD的对角线AC与BD相交于点O,点E、F在对角线AC上,且AF=CE.试问BE∥FD吗?说说你的理由.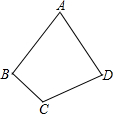 如图是一块四边形的薄钢板,∠A=60°,∠C=120°,AB=AD.
如图是一块四边形的薄钢板,∠A=60°,∠C=120°,AB=AD.
 如图,凸四边形有
如图,凸四边形有