Question

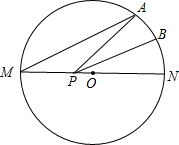
如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，B为AN弧的中点，P是直径MN上一动点，则PA+PB的最小值为

2

．

Answer 1

分析：首先利用在直线L上的同侧有两个点A、B，在直线L上有到A、B的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L的交点就是所要找的点P的位置，然后根据弧的度数发现一个等腰直角三角形计算．

解答：解：作点B关于MN的对称点C，连接AC交MN于点P，则P点就是所求作的点．
此时PA+PB最小，且等于AC的长．
连接OA，OC，根据题意得：
∵∠AMN=30°，
∴弧AN的度数是60°，
∵B为AN弧的中点，
∴弧BN的度数是30°，
∵NO⊥BC，
∴

BN

=

CN

，
∴弧CN的度数是30°，
∴

AC

=

AN

+

CN

=90°
∴∠AOC=90°，
又∵OA=OC=1，
∴AC=

12+12

=

2

．
即PA+PB的最小值为：

2

，
故答案为：

2

．

点评：此题主要考查了利用轴对称求最短路线问题，解答此题的关键是找到点B的对称点，把题目的问题转化为两点之间线段最短解答．