题目内容
材料:为解方程x4-x2-6=0,可将方程变形为(x2)2-x2-6=0,然后设x2=y,则(x2)2=y2,原方程化为y2-y-6=0…①,解得y1=-2,y2=3.当y1=-2时,x2=-2无意义,舍去;当y2=3时,x2=3,解得x=± .所以原方程的解为x1=
.所以原方程的解为x1= ,x2=-
,x2=- .
.
问题:(1)在原方程得到方程①的过程中,利用______法达到了降次的目的,体现了______ 的数学思想;
(2)利用本题的解题方法,解方程(x2-x)2-4(x2-x)-12=0.
解:(1)由题意得:换元 转化;
(2)设x2-x=A,将原方程变形为A2-4A-12=0
解得:A1=6,A2=-2,
当A=6时,
x2-x=6,
解得:
x1=-2,x2=3;
当A=-2时,
x2-x=-2
∵△=1-8=-7<0,
∴原方程无解,
∴原方程的解是:x1=-2,x2=3.
故答案为:换元,转化.
分析:(1)通过阅读材料就可以得出材料中的解法是采用的换元降次的方法从而可以得出结论,
(2)设x2-x=A,将原方程变形为A2-4A-12=0,求出A的值,就可以求出x的值.
点评:本题考查换元法解一元二次方程的运用,根的判别式的运用,在解答时运用换元的方法降次是解答一元高次方程常用的方法.
(2)设x2-x=A,将原方程变形为A2-4A-12=0
解得:A1=6,A2=-2,
当A=6时,
x2-x=6,
解得:
x1=-2,x2=3;
当A=-2时,
x2-x=-2
∵△=1-8=-7<0,
∴原方程无解,
∴原方程的解是:x1=-2,x2=3.
故答案为:换元,转化.
分析:(1)通过阅读材料就可以得出材料中的解法是采用的换元降次的方法从而可以得出结论,
(2)设x2-x=A,将原方程变形为A2-4A-12=0,求出A的值,就可以求出x的值.
点评:本题考查换元法解一元二次方程的运用,根的判别式的运用,在解答时运用换元的方法降次是解答一元高次方程常用的方法.

练习册系列答案
相关题目
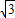 .
.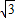 ,x2=-
,x2=-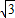 .
.