题目内容
底面直径为6cm的圆锥的侧面展开图的圆心角为216°，则这个圆锥的高为（ ）
分析：圆锥的展开图为扇形，根据弧长公式l=|α|R，可求出扇形的半径，继而利用勾股定理可求出圆锥的高．
解答：解：由题意得，扇形的半径=
=
=5cm，
即AB=5cm，
过点A作AD⊥BC与点D，
在RT△ABD中，AD=
=
=4cm，
即圆锥的高为4cm．
故选D．
| l |
| |α| |
| 6π | ||
|
即AB=5cm，
过点A作AD⊥BC与点D，
在RT△ABD中，AD=
| AB2-BD2 |
| AB2-(R)2 |
即圆锥的高为4cm．
故选D．
点评：此题考查了圆锥的计算，解答本题的关键是求出圆锥展开图图的扇形的半径，然后利用勾股定理求圆锥的高，难度一般．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
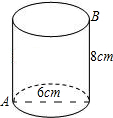如图，一个圆桶儿，底面直径为6cm，高为8cm，则一只小虫从底部点A沿表面爬到上底B处，则小虫所爬的最短路径长是
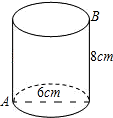如图，一个圆桶儿，底面直径为6cm，高为8cm，则一只小虫从底部点A沿表面爬到上底B处，则小虫所爬的最短路径长是________．（用π表示最后结果）