题目内容
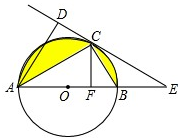 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB,延长AB交DC于点E.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB,延长AB交DC于点E.
(1)求证:直线DE与⊙O相切;
(2)求证:AC2=AD•AB;
(3)若AC=2 ,AB-AD=2,求sin∠BCE的值.
,AB-AD=2,求sin∠BCE的值.
(1)证明: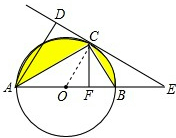 连接OC,
连接OC,
∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥ED,
∴OC⊥DE,
∵OC为半径,
∴DE是⊙O的切线.
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵AD⊥DE,
∴∠ADC=90°=∠ACB,
∵∠DAC=∠BAC,
∴△ACD∽△ABC,
∴ =
= ,
,
∴AC2=AD•AB.
(3)解:设AD=x,则AB=x+2,
∵AC2=AD•AB.,
∴(2 )2=x(x+2),整理得x2+2x-24=0,
)2=x(x+2),整理得x2+2x-24=0,
解得x1=4,x2=-6(舍),
∴AD=4,
∵∠ADC=∠ACB=90°,
∴∠DAC+∠DCA=90°,∠DCA+∠BCE=90°,
∴∠DAC=∠BCE,
∴cos∠BCE=cos∠DAC= =
=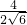 =
= .
.
分析:(1)连接OC,根据已知推出∠DAC=∠BAC=∠OCA,推出OC∥AD,推出OC⊥ED,根据切线判定推出即可;
(2)证△ADC∽△ACB,得出比例式,即可得出答案;
(3)根据AC2=AD•AB求出AD长,求出∠DAC=∠BCE,在Rt△DAC中,解直角三角形求出即可.
点评:本题考查了平行线的性质和判定,切线的判定,圆周角定理,相似三角形的性质和判定,等腰三角形的性质,锐角三角函数的定义的应用,主要考查学生综合运用性质进行推理和计算的能力.
 连接OC,
连接OC,∵OA=OC,
∴∠OCA=∠OAC,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥ED,
∴OC⊥DE,
∵OC为半径,
∴DE是⊙O的切线.
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵AD⊥DE,
∴∠ADC=90°=∠ACB,
∵∠DAC=∠BAC,
∴△ACD∽△ABC,
∴
 =
= ,
,∴AC2=AD•AB.
(3)解:设AD=x,则AB=x+2,
∵AC2=AD•AB.,
∴(2
 )2=x(x+2),整理得x2+2x-24=0,
)2=x(x+2),整理得x2+2x-24=0,解得x1=4,x2=-6(舍),
∴AD=4,
∵∠ADC=∠ACB=90°,
∴∠DAC+∠DCA=90°,∠DCA+∠BCE=90°,
∴∠DAC=∠BCE,
∴cos∠BCE=cos∠DAC=
 =
=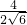 =
= .
.分析:(1)连接OC,根据已知推出∠DAC=∠BAC=∠OCA,推出OC∥AD,推出OC⊥ED,根据切线判定推出即可;
(2)证△ADC∽△ACB,得出比例式,即可得出答案;
(3)根据AC2=AD•AB求出AD长,求出∠DAC=∠BCE,在Rt△DAC中,解直角三角形求出即可.
点评:本题考查了平行线的性质和判定,切线的判定,圆周角定理,相似三角形的性质和判定,等腰三角形的性质,锐角三角函数的定义的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为