题目内容
在△ABC与△A′B′C′中,∠A=30°,∠B=45°,且△ABC≌△A′B′C′,则∠C′=________.
105°
分析:根据全等三角形的性质和三角形的内角和定理,解答出即可.
解答:∵△ABC≌△A′B′C′,
∴∠A=∠A′,∠B=∠B′,
∵∠A=30°,∠B=45°,
∴∠A′=30°,∠B′=45°,
∴∠C′=180°-∠A′-∠B′
=180°-30°-45°
=105°.
故答案为:105°.
点评:本题主要考查了全等三角形的性质和三角形的内角和定理,知道全等三角形的对应角相等和三角形的内角和是180°.
分析:根据全等三角形的性质和三角形的内角和定理,解答出即可.
解答:∵△ABC≌△A′B′C′,
∴∠A=∠A′,∠B=∠B′,
∵∠A=30°,∠B=45°,
∴∠A′=30°,∠B′=45°,
∴∠C′=180°-∠A′-∠B′
=180°-30°-45°
=105°.
故答案为:105°.
点评:本题主要考查了全等三角形的性质和三角形的内角和定理,知道全等三角形的对应角相等和三角形的内角和是180°.

练习册系列答案
相关题目
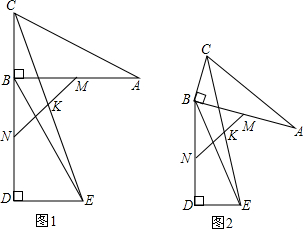
 如图,在△ABC与△ADE中,∠C=∠E,∠1=∠2,AC=AD=2AB=6,求AE的长.
如图,在△ABC与△ADE中,∠C=∠E,∠1=∠2,AC=AD=2AB=6,求AE的长. 如图,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
如图,在△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论: 如图,在△ABC与△DEF中,给出下列条件①
如图,在△ABC与△DEF中,给出下列条件① 如图,在△ABC与△DCB中,∠A=∠D,要使△ABC≌△DCB,需要添加的一个条件是
如图,在△ABC与△DCB中,∠A=∠D,要使△ABC≌△DCB,需要添加的一个条件是