题目内容
甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶,甲车先到达B地,停留1小时后按原路以另一速度匀速返回,直到两车相遇,乙车的速度为每小时120千米,下图是两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象.(1)请将图中的______内填上正确的值,并直接写出甲车从A到B的行驶速度.
(2)求从甲车返回到乙车相遇过程中y与x之间的函数关系式,并写出自变量x的取值范围.
(3)求出甲车返回时行驶速度及A、B两地的距离.
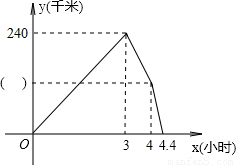
【答案】分析:(1)3小时时,甲车到达B地,3小时和4小时之间是甲车停留的1小时,乙车的速度为每小时120千米,则4小时时,两车相距120千米,即为( )所填写的内容;根据3小时内两车的路程差是240千米,得1小时两车的路程差是80千米,又乙车的速度是每小时120千米,即可求得甲车的速度;
(2)设解析式为y=kx+b,把已知坐标(4.4,0)和(4,120)代入可求解.根据横坐标的x的取值范围可知自变量x的取值范围;
(3)设甲车返回行驶速度为v千米/时,根据两车用0.4小时共同开了120km即可求解;根据(1)中求得的甲的速度和甲3小时到达B地即可求得两地的距离.
解答:解:(1)由图中可以看出,甲乙两车在3小时时相距240千米,然后只剩下乙车行走,乙车1小时行走120千米,所以4小时时,两车相距120千米;
∵3小时两车相距240千米,
∴1小时两车相距80千米,
∵乙车的速度为每小时120千米,
∴甲车的速度为200千米/时,
故答案为120.
(2)设y与x之间的函数关系式为y=kx+b,
 ,
,
解得: ,
,
∴y=-300x+1320(4≤x≤4.4);
(3)∵两车用0.4小时共同开了120km,乙车的速度为120千米/时,
∴两车1小时共开了300千米,
∴甲车的速度为180千米/时,
A、B两地的距离为200×3=600千米.
点评:考查一次函数的应用;理解函数图象的横轴和纵轴表示的意义是解决本题的突破点.
(2)设解析式为y=kx+b,把已知坐标(4.4,0)和(4,120)代入可求解.根据横坐标的x的取值范围可知自变量x的取值范围;
(3)设甲车返回行驶速度为v千米/时,根据两车用0.4小时共同开了120km即可求解;根据(1)中求得的甲的速度和甲3小时到达B地即可求得两地的距离.
解答:解:(1)由图中可以看出,甲乙两车在3小时时相距240千米,然后只剩下乙车行走,乙车1小时行走120千米,所以4小时时,两车相距120千米;
∵3小时两车相距240千米,
∴1小时两车相距80千米,
∵乙车的速度为每小时120千米,
∴甲车的速度为200千米/时,
故答案为120.
(2)设y与x之间的函数关系式为y=kx+b,
 ,
,解得:
 ,
,∴y=-300x+1320(4≤x≤4.4);
(3)∵两车用0.4小时共同开了120km,乙车的速度为120千米/时,
∴两车1小时共开了300千米,
∴甲车的速度为180千米/时,
A、B两地的距离为200×3=600千米.
点评:考查一次函数的应用;理解函数图象的横轴和纵轴表示的意义是解决本题的突破点.

练习册系列答案
相关题目
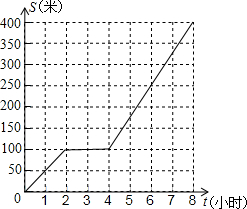 地的路程s (千米)与时间t (小时) 的关系如图所示.
地的路程s (千米)与时间t (小时) 的关系如图所示.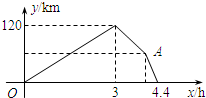 车之间的距离y(km)与乙车行驶时间x(h)之间的函数图象.以下结论正确的是
车之间的距离y(km)与乙车行驶时间x(h)之间的函数图象.以下结论正确的是 A、B两地相距800km,甲、乙两车同时从A地出发驶向B地.甲车到达B地后立即返回,如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.
A、B两地相距800km,甲、乙两车同时从A地出发驶向B地.甲车到达B地后立即返回,如图是它们离A地的距离y(km)与行驶时间x(h)之间的函数图象.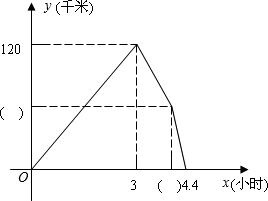 甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为40km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下,则甲车从A到B的速度为
甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶.甲车先到达B地,停留一小时后按原路以另一速度匀速返回,直到两车相遇.乙车的速度为40km/h,两车间距离y(km)与乙车行驶时间x(h)之间的函数图象如下,则甲车从A到B的速度为