Question

【题目】我们知道一次函数 与 的图象关于 轴对称，所以我们定义：函数 与 互为“镜子”函数．

（1）请直接写出函数 的“镜子”函数
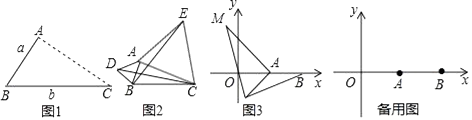
（2）如果一对“镜子”函数 与 的图象交于点 ，且与 轴交于 、 两点，如图所示，若 ，且 的面积是 ，求这对“镜子”函数的解析式．
（3）若点 是 轴上的一个动点，当 为等腰三角形时，直接写出点 的坐标．

Answer 1

【答案】
（1）解：根据题意，“镜子函数”为关于 轴对称的两个函数，

∴原函数的“镜子函数”为

（2）解：根据题意， 和 为一对“镜子函数”．

∴ ，即 为等腰直角三角形，

即 ，

∴ ，

又∵ 且 ，

∴解得 ，

那么 和

（3）解：根据等腰三角形的性质，分情况，

∵ ， ，

∴以 为顶点，则 ，得 ， ，

以 为顶点，则 ，得 ，

以 为顶点，则 ，得

【解析】（1）根据“镜子”函数的定义，即可得出结果。
（2）（2）根据已知条件可证得△ABC是等腰直角三角形，得出OA=OB=OC，再根据△ABC的面积是8，就可得出点A、B、C的坐标，利用待定系数法即可求出这对“镜子函数”的解析式。
（3）根据等腰三角形的性质，分为三种情况讨论：当点A为顶点时；当点B为顶点时；当D为顶点时，根据AB、AO、BO的长，即可求出点D的坐标。