题目内容
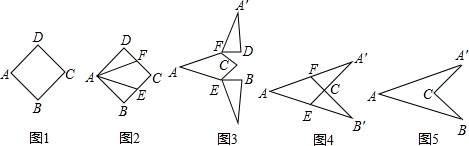
如图1，正方形ABCD中，AB=2，图2到图5是将该正方形变换成以直线AC为对称轴的轴对称图形“箭头”，则图5中AA′的长为________．
2
分析：根据轴对称变换和性质得到图2中的Rt△ADF、图3中的Rt△A′DF和图4中的Rt△A′FC都全等，并且FC=DF，则AF=A′F，然后在Rt△ADF中利用勾股定理计算出AF，即可得到AA′．
解答：根据图中变换，图2中的Rt△ADF、图3中的Rt△A′DF和图4中的Rt△A′FC都全等，并且FC=DF，
∴AF=A′F，
在Rt△ADF中，AD=AB=DC=2，DF=FC=1，
AF=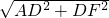
=
=，
∴AA′=2AF=2．
故答案为2．
点评：本题考查了轴对称的性质：轴对称图形的对应线段相等，对应角相等，对应点的连线段被对称轴垂直平分．也考查了勾股定理以及正方形的性质．
分析：根据轴对称变换和性质得到图2中的Rt△ADF、图3中的Rt△A′DF和图4中的Rt△A′FC都全等，并且FC=DF，则AF=A′F，然后在Rt△ADF中利用勾股定理计算出AF，即可得到AA′．
解答：根据图中变换，图2中的Rt△ADF、图3中的Rt△A′DF和图4中的Rt△A′FC都全等，并且FC=DF，
∴AF=A′F，
在Rt△ADF中，AD=AB=DC=2，DF=FC=1，
AF=
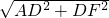==，∴AA′=2AF=2
．故答案为2
．点评：本题考查了轴对称的性质：轴对称图形的对应线段相等，对应角相等，对应点的连线段被对称轴垂直平分．也考查了勾股定理以及正方形的性质．
练习册系列答案
相关题目
21、如图，在正方形网格上的一个△ABC．（其中点A、B、C均在网格上）
（2012•安庆一模）如图，等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动．如果MN=2AC=4cm，那么△ABC和正方形XYMN重叠部分的面积S（cm2）与匀速运动所用时间t（min）之间的函数的大致图象是（ ）
如图，以Rt△ABC的斜边和一直角边为边长向外作正方形，面积分别为169和25，则另一直角边的长度BC为（ ）