题目内容
【题目】如图,在△ABC中,点D为BC上一点,点P在AD上,过点P作PM∥AC交AB于点M,作PN∥AB交AC于点N.
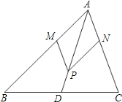
(1)若点D是BC的中点,
①若AP:PD=2:1,求AM:AB的值
②证明:![]() ;
;
(2)若点D是BC上任意一点,试证明:![]() .
.
【答案】(1)①![]() ;②见解析;(2)见解析.
;②见解析;(2)见解析.
【解析】
(1)①过点D作DE∥PM交AB于E,由点D为BC中点与AP:PD=2:1,根据平行线分线段成比例定理,即可求得AM:AB的值;
②延长AD至点Q,使DQ=AD,连BQ、CQ,易得四边形ABQC是平行四边形,由平行四边形的性质可得PM∥BQ,PN∥CQ,继而可得![]() ;
;
(2)过点D作DE∥PM交AB于E,即可得![]() ,又由PM∥AC,根据平行线分线段成比例定理可得
,又由PM∥AC,根据平行线分线段成比例定理可得![]() ,继而求得
,继而求得![]() .
.
(1)①过点D作DE∥PM交AB于E,

∵PM∥AC,∴DE∥AC,
![]() .
.
∵点D为BC中点,
∴点E是AB中点,且![]() ,
,
∴![]() ;
;
②延长AD至点Q,使DQ=AD,连BQ、CQ,

∵DQ=AD,BD=DC,
![]() 四边形ABQC是平行四边形.
四边形ABQC是平行四边形.
∴PM∥BQ,PN∥CQ,
∴![]() ,
,![]() ,
,
∴![]() ;(注:像第(1)题那样作辅助线也可以.)
;(注:像第(1)题那样作辅助线也可以.)
(3)过点D作DE∥PM交AB于E,

∴![]() ,
,
又∵PM∥AC,∴DE∥AC,
∴![]() ,
,
∴![]() ,
,
同理可得:![]() ,
,
∴![]() .
.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目