题目内容
根据对某市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的甲种蔬菜的销售利润y1(千元)与进货量x(吨)之间的函数 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数 的图象如图②所示.
的图象如图②所示.
(1)分别求出y1、y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种蔬菜共10吨,设乙种蔬菜的进货量为t吨,写出这
两种蔬菜所获 得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种蔬菜各进多少吨时获得的销售利润之和最大,最大利润是多少?
得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种蔬菜各进多少吨时获得的销售利润之和最大,最大利润是多少?


解:(1) .------------------------------------------------------------------2
.------------------------------------------------------------------2
∵抛物线y=ax2+bx经过点B(1,2)、C(5,6)
 ∴
∴  ----------------------------------------------------------3
----------------------------------------------------------3
∴ -----------------------------------------------------------------5
-----------------------------------------------------------------5
∴ .-----------------------------------------------------------6
.-----------------------------------------------------------6
(2) --------------------------------------
-------------------------------------- ---------------7
---------------7
 .--------------------------------------------------------8
.--------------------------------------------------------8
 .--------------------------------------------------------9
.--------------------------------------------------------9
∵a=-0.2<0,抛物线开口向下
∴当t=4时,W有最大值9.2---------------------------------------------11
答:甲种蔬菜进货量为6吨,乙种蔬菜进货量为4吨时,获得的销售利润之和最大,最大利润是9200元. -----------------------------------------------------12

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案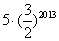 B.
B.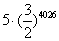 C.
C.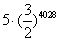 D.
D.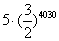
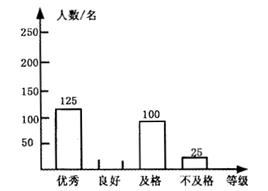
 行50米跑测试,并根据测试结果绘制了如下尚
行50米跑测试,并根据测试结果绘制了如下尚
 的值,其中
的值,其中



 A. B. C. D.
A. B. C. D.