题目内容
不等于0的三个数a、b、c满足| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a+b+c |
分析:直接通分,将分式等式转化为整式等式,再因式分解得到(b+c)(a+b)(a+c)=0,可知其中至少有一个因式为0.
解答:证明:∵
+
+
=
∴
=
bc(a+b+c)+ac(a+b+c)+ab(a+b+c)=abc
∴(b+c)a2+(2bc+c2+b2)a+bc2+b2c=0
即(a2b+ab2)+(a2c+ac2)+(abc+bc2)+(abc+b2c)=0,
ab(a+b)+ac(a+c)+bc(a+c)+bc(a+b)=0,
(a+b)(ab+bc)+(a+c)(ac+bc)=0,
b(a+b)(a+c)+c(a+c)(a+b)=0,
∴(b+c)(a+b)(a+c)=0
∴b=-c或a=-b或a=-c.
即a、b、c中至少有两个互为相反数.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| a+b+c |
∴
| ac+bc+ab |
| abc |
| 1 |
| a+b+c |
bc(a+b+c)+ac(a+b+c)+ab(a+b+c)=abc
∴(b+c)a2+(2bc+c2+b2)a+bc2+b2c=0
即(a2b+ab2)+(a2c+ac2)+(abc+bc2)+(abc+b2c)=0,
ab(a+b)+ac(a+c)+bc(a+c)+bc(a+b)=0,
(a+b)(ab+bc)+(a+c)(ac+bc)=0,
b(a+b)(a+c)+c(a+c)(a+b)=0,
∴(b+c)(a+b)(a+c)=0
∴b=-c或a=-b或a=-c.
即a、b、c中至少有两个互为相反数.
点评:本题考查了分式加减运算的运用,先通分,去分母,将分式等式转化为整式等式,再运用因式分解的知识解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



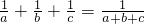 ,求证:a、b、c中至少有两个互为相反数.
,求证:a、b、c中至少有两个互为相反数.