题目内容
解方程(组):
(1)
(2) .
.
(1)
解:使方程(1)×5-(2)×2得,31x=62,解得,x=2;
将x=2代入方程(1)中得,y= =1
=1
∴原方程组的解为: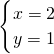 .
.
(2)
解:方程两边都乘以x(x-1),得:x2+2(x-1)=x(x-1),
解这个方程,得x=
经检验,x= 是原方程的根.
是原方程的根.
分析:(1)解二元一次方程组,分别是两个方程乘以不同的数,但保证乘以不同的数后y有相同的系数,消去y得到关于x的一元一次方程,解之求出x的值,将x的值代入原方程组的任一个方程求出y的值,即求出了原方程组的解;
(2)解分式方程,首先去分母,使得方程两边同乘以分母的最小公倍数,得到一个关于x的方程,求解即可.
点评:本题考查的二元一次方程组和分式方程的求解问题,在求解的过程中应注意:所求得的方程组的解代入原方程组看是否满足,方程两边同乘以分母的最小公倍数,分子作为一整体加括号,注意分式方程一定要验根.

解:使方程(1)×5-(2)×2得,31x=62,解得,x=2;
将x=2代入方程(1)中得,y=
 =1
=1∴原方程组的解为:
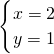 .
.(2)

解:方程两边都乘以x(x-1),得:x2+2(x-1)=x(x-1),
解这个方程,得x=

经检验,x=
 是原方程的根.
是原方程的根.分析:(1)解二元一次方程组,分别是两个方程乘以不同的数,但保证乘以不同的数后y有相同的系数,消去y得到关于x的一元一次方程,解之求出x的值,将x的值代入原方程组的任一个方程求出y的值,即求出了原方程组的解;
(2)解分式方程,首先去分母,使得方程两边同乘以分母的最小公倍数,得到一个关于x的方程,求解即可.
点评:本题考查的二元一次方程组和分式方程的求解问题,在求解的过程中应注意:所求得的方程组的解代入原方程组看是否满足,方程两边同乘以分母的最小公倍数,分子作为一整体加括号,注意分式方程一定要验根.

练习册系列答案
相关题目