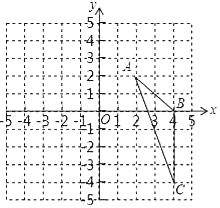
ЬтФПФкШн
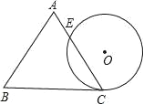
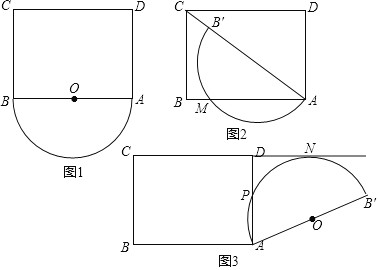
ЁОЬтФПЁПвбжЊОиаЮABCDЃЌAB=4ЃЌBC=3ЃЌвдABЮЊжБОЖЕФАыдВOдкОиаЮABCDЕФЭтВПЃЈШчЭМЃЉЃЌНЋАыдВOШЦЕуAЫГЪБеыа§зЊІСЖШЃЈ0ЁуЁмІСЁм180ЁуЃЉ
ЃЈ1ЃЉАыдВЕФжБОЖТфдкЖдНЧЯпACЩЯЪБЃЌШчЭМЫљЪОЃЌАыдВгыABЕФНЛЕуЮЊMЃЌЧѓAMЕФГЄЃЛ
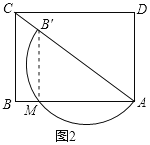
ЃЈ2ЃЉАыдВгыжБЯпCDЯрЧаЪБЃЌЧаЕуЮЊNЃЌгыЯпЖЮADЕФНЛЕуЮЊPЃЌШчЭМЫљЪОЃЌЧѓСгЛЁAPЕФГЄЃЛ
ЃЈ3ЃЉдка§зЊЙ§ГЬжаЃЌАыдВЛЁгыжБЯпCDжЛгавЛИіНЛЕуЪБЃЌЩшДЫНЛЕугыЕуCЕФОрРыЮЊdЃЌжБНгаДГіdЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉAM=![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() =
=![]() ІаЃЛЃЈ3ЃЉ4-
ІаЃЛЃЈ3ЃЉ4-![]() ЁмdЃМ4Лђd=4+
ЁмdЃМ4Лђd=4+![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
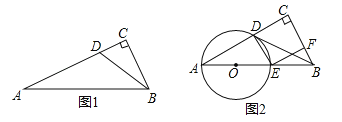
ЃЈ1ЃЉСЌНгBЁфMЃЌдђЁЯBЁфMA=90ЁуЃЌдкRtЁїABCжаЃЌРћгУЙДЙЩЖЈРэПЩЧѓГіACЕФГЄЖШЃЌгЩЁЯB=ЁЯBЁфMA=90ЁуЁЂЁЯBCA=ЁЯMABЁфПЩЕУГіЁїABCЁзЁїAMBЁфЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪПЩЧѓГіAMЕФГЄЖШЃЛ
ЃЈ2ЃЉСЌНгOPЁЂONЃЌЙ§ЕуOзїOGЁЭADгкЕуGЃЌдђЫФБпаЮDGONЮЊОиаЮЃЌНјЖјПЩЕУГіDGЁЂAGЕФГЄЖШЃЌдкRtЁїAGOжаЃЌгЩAO=2ЁЂAG=1ПЩЕУГіЁЯOAG=60ЁуЃЌНјЖјПЩЕУГіЁїAOPЮЊЕШБпШ§НЧаЮЃЌдйРћгУЛЁГЄЙЋЪНМДПЩЧѓГіСгЛЁAPЕФГЄЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊЃКЁїAOPЮЊЕШБпШ§НЧаЮЃЌИљОнЕШБпШ§НЧаЮЕФаджЪПЩЧѓГіOGЁЂDNЕФГЄЖШЃЌНјЖјПЩЕУГіCNЕФГЄЖШЃЌЛГіЕуBЁфдкжБЯпCDЩЯЕФЭМаЮЃЌдкRtЁїABЁфDжаЃЈЕуBЁфдкЕуDзѓБпЃЉЃЌРћгУЙДЙЩЖЈРэПЩЧѓГіBЁфDЕФГЄЖШНјЖјПЩЕУГіCBЁфЕФГЄЖШЃЌдйНсКЯЭМаЮМДПЩЕУГіЃКАыдВЛЁгыжБЯпCDжЛгавЛИіНЛЕуЪБdЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉдкЭМ2жаЃЌСЌНгBЁфMЃЌдђЁЯBЁфMA=90ЁуЃЎ
дкRtЁїABCжаЃЌAB=4ЃЌBC=3ЃЌ
ЁрAC=5ЃЎ
ЁпЁЯB=ЁЯBЁфMA=90ЁуЃЌЁЯBCA=ЁЯMABЁфЃЌ
ЁрЁїABCЁзЁїAMBЁфЃЌ
Ёр![]() =
=![]() ЃЌМД
ЃЌМД![]() =
=![]() ЃЌ
ЃЌ
ЁрAM=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉдкЭМ3жаЃЌСЌНгOPЁЂONЃЌЙ§ЕуOзїOGЁЭADгкЕуGЃЌ
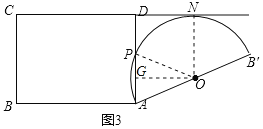
ЁпАыдВгыжБЯпCDЯрЧаЃЌ
ЁрONЁЭDNЃЌ
ЁрЫФБпаЮDGONЮЊОиаЮЃЌ
ЁрDG=ON=2ЃЌ
ЁрAG=AD-DG=1ЃЎ
дкRtЁїAGOжаЃЌЁЯAGO=90ЁуЃЌAO=2ЃЌAG=1ЃЌ
ЁрЁЯAOG=30ЁуЃЌЁЯOAG=60ЁуЃЎ
гжЁпOA=OPЃЌ
ЁрЁїAOPЮЊЕШБпШ§НЧаЮЃЌ
Ёр![]() =
=![]() =
=![]() ІаЃЎ
ІаЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊЃКЁїAOPЮЊЕШБпШ§НЧаЮЃЌ
ЁрDN=GO=![]() OA=
OA=![]() ЃЌ
ЃЌ
ЁрCN=CD+DN=4+![]() ЃЎ
ЃЎ
ЕБЕуBЁфдкжБЯпCDЩЯЪБЃЌШчЭМ4ЫљЪОЃЌ
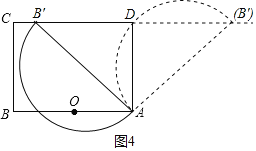
дкRtЁїABЁфDжаЃЈЕуBЁфдкЕуDзѓБпЃЉЃЌABЁф=4ЃЌAD=3ЃЌ
ЁрBЁфD=![]() =
=![]() ЃЌ
ЃЌ
ЁрCBЁф=4-![]() ЃЎ
ЃЎ
ЁпABЁфЮЊжБОЖЃЌ
ЁрЁЯADBЁф=90ЁуЃЌ
ЁрЕБЕуBЁфдкЕуDгвБпЪБЃЌАыдВНЛжБЯпCDгкЕуDЁЂBЁфЃЎ
ЁрЕБАыдВЛЁгыжБЯпCDжЛгавЛИіНЛЕуЪБЃЌ4-![]() ЁмdЃМ4Лђd=4+
ЁмdЃМ4Лђd=4+![]() ЃЎ
ЃЎ