Question

在△ABC中，已知∠A、∠B、∠C的度数之比是1：2：3，AB=6，求AC的长．

Answer 1

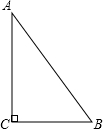解：∵在△ABC中，∠A：∠B：∠C=1：2：3，∠A+∠B+∠C=180°，
∴∠A=30°，∠C=90°，即△ABC是直角三角形．
又∵AB=6，
∴AC=AB•cosA=6×=3．
即线段AC的长度是3．
分析：根据三角形内角和定理与已知条件推知△ABC是含30度角的直角三角形，通过30度角的余弦函数的定义来求线段AC的长度．
点评：本题考查了解直角三角形．解题时，要熟练掌握好边角之间的关系．