题目内容
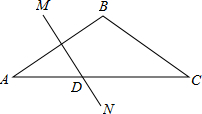 (2004•呼和浩特)如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC于D,求证:AD=
(2004•呼和浩特)如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC于D,求证:AD=| 1 | 2 |
分析:连接BD,根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,然后求出∠A=∠C=∠ABD=30°,再求出∠DBC=90°,再根据直角三角形30°所对的直角边等于斜边的一半即可得证.
解答: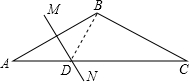 解:如图,连接DB.
解:如图,连接DB.
∵MN是AB的垂直平分线,
∴AD=DB,
∴∠A=∠ABD,
∵BA=BC,∠B=120°,
∴∠A=∠C=
(180°-120°)=30°,
∴∠ABD=30°,
又∵∠ABC=120°,
∴∠DBC=120°-30°=90°,
∴BD=
DC,
∴AD=
DC.
 解:如图,连接DB.
解:如图,连接DB.∵MN是AB的垂直平分线,
∴AD=DB,
∴∠A=∠ABD,
∵BA=BC,∠B=120°,
∴∠A=∠C=
| 1 |
| 2 |
∴∠ABD=30°,
又∵∠ABC=120°,
∴∠DBC=120°-30°=90°,
∴BD=
| 1 |
| 2 |
∴AD=
| 1 |
| 2 |
点评:本题考查了30°角所对的直角边等于斜边的一半的性质,线段垂直平分线上的点到线段两端点的距离相等的性质,作出辅助线构造出直角三角形是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 (2004•呼和浩特)如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是( )
(2004•呼和浩特)如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是( )