题目内容
等腰三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根,则n的值为
( )
A.9 B.10 C.9或10 D.8或10
B【考点】根的判别式;一元二次方程的解;等腰直角三角形.
【分析】由三角形是等腰三角形,得到①a=2,或b=2,②a=b①当a=2,或b=2时,得到方程的根x=2,把x=2代入x2﹣6x+n﹣1=0即可得到结果;②当a=b时,方程x2﹣6x+n﹣1=0有两个相等的实数根,由△=(﹣6)2﹣4(n﹣1)=0可的结果.
【解答】解:∵三角形是等腰三角形,
∴①a=2,或b=2,②a=b两种情况,
①当a=2,或b=2时,
∵a,b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根,
∴x=2,
把x=2代入x2﹣6x+n﹣1=0得,22﹣6×2+n﹣1=0,
解得:n=9,
当n=9,方程的两根是2和4,而2,4,2不能组成三角形,
故n=9不合题意,
②当a=b时,方程x2﹣6x+n﹣1=0有两个相等的实数根,
∴△=(﹣6)2﹣4(n﹣1)=0
解得:n=10,
故选B.
【点评】本题考查了等腰直角三角形的性质,一元二次方程的根,一元二次方程根的判别式,注意分类讨论思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



 x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.
x2+bx+c经过B、C两点,点D为抛物线的顶点,连接AC、BD、CD.

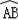
 的长为2π,则∠ACB的大小是 .
的长为2π,则∠ACB的大小是 .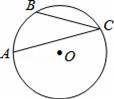


 B.
B.
 C.
C.
 D.
D.




 ÷(2﹣
÷(2﹣
 ),其中x=
),其中x=
 +1.
+1.