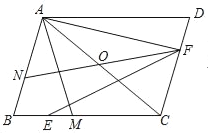
题目内容
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是平面上的一点,且
是平面上的一点,且![]() ,连接
,连接![]() .
.
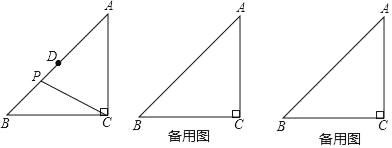
(1)如图,当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 的长;
的长;
(2)当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的长;
的长;
(3)将点![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到点
得到点![]() ,连接
,连接![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)2![]() ;(2)见解析;(3)
;(2)见解析;(3) ![]() .
.
【解析】
(1)根据勾股定理求出AB的长,由直角三角形斜边中线的性质可求出CD的长,利用勾股定理求出PC的长即可;(2)由DP=1可知点P在以D为圆心,1为半径的圆上,分别讨论![]() 、
、![]() 、
、![]() 的情况,求出PC的长即可;(3)由旋转性质可知
的情况,求出PC的长即可;(3)由旋转性质可知![]() ,
,![]() ,可得
,可得![]() ,由等腰直角三角形的性质可知
,由等腰直角三角形的性质可知![]() ,进而可证明
,进而可证明![]() ∽
∽![]() ,即可得
,即可得![]() ,利用三角形三边关系即可得答案.
,利用三角形三边关系即可得答案.
(1)如图1中,连接![]() .
.
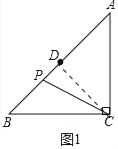
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() .
.
(2)如图2中,∵![]() ,
,
∴点![]() 在以点
在以点![]() 为圆心的⊙
为圆心的⊙![]() 上.
上.
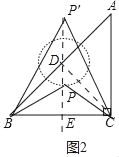
①当![]() 时,
时,
∵![]() ,
,
∴![]() 都在线段
都在线段![]() 的垂直平分线上,设直线
的垂直平分线上,设直线![]() 交
交![]() 于
于![]() .
.
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
当![]() 在线段
在线段![]() 上时,
上时,![]() ,
,![]() ,
,
当![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ,
,![]() .
.
②当![]() 时,∵
时,∵![]() ,
,
∴![]() ,此种情形不存在;
,此种情形不存在;
③当![]() 时,同理这种情形不存在;
时,同理这种情形不存在;
如图3中
(3)如图4中,连接![]() .
.
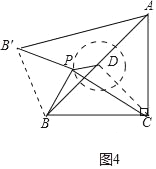
由旋转可知:![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴点![]() 落在
落在![]() 的延长线与⊙
的延长线与⊙![]() 的交点处,
的交点处,![]() 的值最大,
的值最大,
∴![]() .
.
∴![]() 的最大值为
的最大值为![]() .
.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】阅读材料:
工厂加工某种新型材料,首先要将材料进行加温处理,使这种材料保持在一定的温度范围内方可进行继续加工![]() 处理这种材料时,材料温度
处理这种材料时,材料温度![]() 是时间
是时间![]() 的函数
的函数![]() 下面是小明同学研究该函数的过程,把它补充完整:
下面是小明同学研究该函数的过程,把它补充完整:
![]() 在这个函数关系中,自变量x的取值范围是______.
在这个函数关系中,自变量x的取值范围是______.
![]() 如表记录了17min内10个时间点材料温度y随时间x变化的情况:
如表记录了17min内10个时间点材料温度y随时间x变化的情况:
时间 | 0 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
|
温度 | 15 | 24 | 42 | 60 |
|
|
|
| m |
|
|
上表中m的值为______.
![]() 如图,在平面直角坐标系xOy中,已经描出了上表中的部分点
如图,在平面直角坐标系xOy中,已经描出了上表中的部分点![]() 根据描出的点,画出该函数的图象.
根据描出的点,画出该函数的图象.
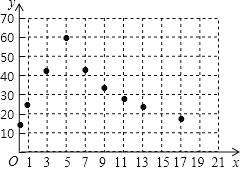
![]() 根据列出的表格和所画的函数图象,可以得到,当
根据列出的表格和所画的函数图象,可以得到,当![]() 时,y与x之间的函数表达式为______,当
时,y与x之间的函数表达式为______,当![]() 时,y与x之间的函数表达式为______.
时,y与x之间的函数表达式为______.
![]() 根据工艺的要求,当材料的温度不低于
根据工艺的要求,当材料的温度不低于![]() 时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.
时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.