题目内容
小明遇到这样一个问题:如图1,在边长为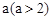 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
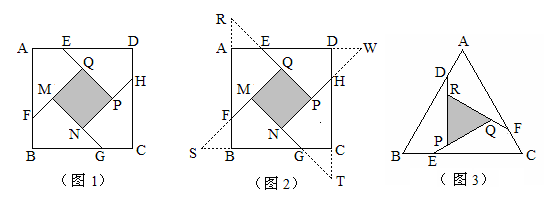
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为 ;
(2)求正方形MNPQ的面积。参考小明思考问题的方法,解决问题:
(3)如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若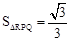 ,则AD的长为 。
,则AD的长为 。
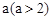 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积。小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为 ;
(2)求正方形MNPQ的面积。参考小明思考问题的方法,解决问题:
(3)如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若
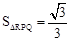 ,则AD的长为 。
,则AD的长为 。(1)a
(2)∵△RQF,△SMG,△TNH,△WPE四个全等的等腰直角三角形面积和为 ,正方形ABCD的面积为
,正方形ABCD的面积为 ,∴
,∴ 。
。
(3)
(2)∵△RQF,△SMG,△TNH,△WPE四个全等的等腰直角三角形面积和为
 ,正方形ABCD的面积为
,正方形ABCD的面积为 ,∴
,∴ 。
。(3)

(1)由△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形可知△AER,△BFS,△CGT,△DHW也是全等的等腰直角三角形,从而得新的正方形的边长FR=FA+AR=FA+AE=FA+BF=a。
(2)由正方形ABCD的面积等于△RQF,△SMG,△TNH,△WPE四个全等的等腰直角三角形面积和可知 。
。
(3)如图,延长DP交BC于点H,

由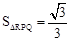 可求得等边△RPQ的边长
可求得等边△RPQ的边长 。
。
设等边△ABC的边长为a,AD=BE=CF=x,则BD=CE= 。
。
由等边三角形的性质和含30度角直角三角形的性质,得
DH= ,BH=
,BH=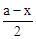 ,EH=
,EH= ,
,
PH= ,DR=EP=
,DR=EP= 。
。
由DH=DR+RP+PH得: ,
,
解得 ,即AD的长为
,即AD的长为 。
。
(2)由正方形ABCD的面积等于△RQF,△SMG,△TNH,△WPE四个全等的等腰直角三角形面积和可知
 。
。(3)如图,延长DP交BC于点H,

由
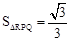 可求得等边△RPQ的边长
可求得等边△RPQ的边长 。
。设等边△ABC的边长为a,AD=BE=CF=x,则BD=CE=
 。
。由等边三角形的性质和含30度角直角三角形的性质,得
DH=
 ,BH=
,BH=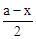 ,EH=
,EH= ,
,PH=
 ,DR=EP=
,DR=EP= 。
。由DH=DR+RP+PH得:
 ,
,解得
 ,即AD的长为
,即AD的长为 。
。
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目



 ,若
,若 ,
, ,则对角线
,则对角线 的长等于
的长等于
