题目内容
 如图,△ABC中,∠C=90°,EA平分∠BAC,ED垂直平分AB,则∠B=
如图,△ABC中,∠C=90°,EA平分∠BAC,ED垂直平分AB,则∠B=考点:线段垂直平分线的性质
专题:
分析:根据线段垂直平分线得出AE=BE,推出∠B=∠BAE,推出∠CAE=∠BAE=∠B,得出3∠B=90°,求出即可.
解答:解:∵ED垂直平分AB,
∴AE=BE,
∴∠B=∠BAE,
∵EA平分∠BAC,
∴∠CAE=∠BAE=∠B,
∵在△ABC中,∠C=90°,
∴3∠B=90°,
∴∠B=30°,
故答案为:30°.
∴AE=BE,
∴∠B=∠BAE,
∵EA平分∠BAC,
∴∠CAE=∠BAE=∠B,
∵在△ABC中,∠C=90°,
∴3∠B=90°,
∴∠B=30°,
故答案为:30°.
点评:本题考查了三角形内角和定理,线段垂直平分线的性质,等腰三角形性质的应用,主要考查学生运用性质进行推理和计算的能力.

练习册系列答案
相关题目
 如图,甲、乙两人分别骑自行车和摩托车沿相同路线由A地到B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
如图,甲、乙两人分别骑自行车和摩托车沿相同路线由A地到B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题: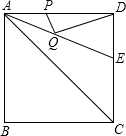 如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为
如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=2cm.则图中阴影部分面积为
如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=2cm.则图中阴影部分面积为 如图,DE∥CB,∠1=30°,∠ADE=85°,则∠BDC=
如图,DE∥CB,∠1=30°,∠ADE=85°,则∠BDC=