题目内容
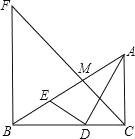
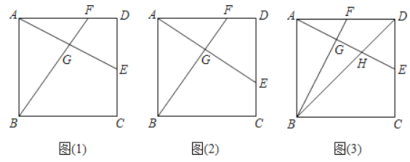
【题目】如图,正方形![]() 的边长为
的边长为![]() 分别是边
分别是边![]() 上的动点,
上的动点,![]() 和
和![]() 交于点
交于点![]() .
.
![]() 如图(1),若
如图(1),若![]() 为边
为边![]() 的中点,
的中点,![]() , 求
, 求![]() 的长;
的长;
![]() 如图(2),若点
如图(2),若点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,点
运动,点![]() 在
在![]() .上从
.上从![]() 向
向![]() 运动.两点同时出发,同时到达各自终点,求在运动过程中,点
运动.两点同时出发,同时到达各自终点,求在运动过程中,点![]() 运动的路径长:
运动的路径长:
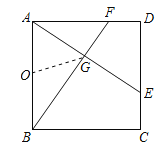
![]() 如图(3), 若
如图(3), 若![]() 分别是边
分别是边![]() 上的中点,
上的中点,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的正切值.
的正切值.
【答案】![]() ;
;![]() ;
;![]()
【解析】
(1)延长BF、CD交于点H,根据勾股定理求出AE,证明△AFB∽△DFH,根据相似三角形的性质求出DH,再证明△AGB∽△EGH,最后根据相似三角形的性质计算即可;
(2)取AB的中点O,连接OG,证明△BAF≌△ADE,再确定∠AGB=90°,再根据直角三角形的性质求出OG,最后运用弧长公式计算即可;
(3)作FQ⊥BD于Q,设正方形的边长为2a,再用a表示出BQ、FQ,最后根据正切的定义即可解答.
解:(1)如图,延长BF、CD交于点H
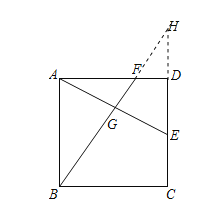
∵E为边CD的中点
∴DE=DC=3
由勾股定理可得![]() ,
,
∵四边形ABCD为正方形
∴AB∥CD
∴△AFB∽△DFH
∴![]()
∵AB=6,
∴DH=3,EH=6
∵AB//CD
∴△AGB∽△EGH,
∴![]()
∴![]() ;
;
(2)如图:
取AB的中点O,连接OG,
由题意可得,AF=DE
在△BAF和△ADE中
BA=AD, ∠BAF=∠ADE,AF=DE
∴△BAF≌△ADE(SAS)
∴∠ABF= ∠DAE
∵∠BAG+ ∠DAE=90°
∴∠BAG+ ∠ABG=90°,即∠AGB=90°
∵点O是AB的中点,
∴OG=![]() AB=3
AB=3
当点E与点C重合、点F与得D重合时,∠AOG=90°
∴点G运动的路径长为:![]() ;
;
(3)如图,作FQ⊥BD于Q,设正方形的边长为2a

∵点F是边AD上的中点
∴AF=DF=a,
∵四边形ABCD为正方形
∴![]() ,∠ADB=45°
,∠ADB=45°
∴![]()
∴![]()
∴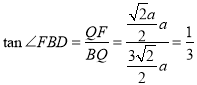 .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目