题目内容
【题目】已知:如图,在正方形ABCD外取点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.
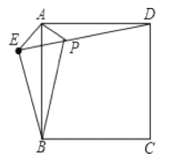
(1)求证:△APD≌△AEB;
(2)连接PC,求线段PC的长度;
(3)试求正方形ABCD的面积。
【答案】(1)见解析(2)![]() (3)2+
(3)2+![]()
【解析】
(1)由四边形ABCD是正方形,得到AB=AD,∠BAD=90°,由AE⊥AP,得到∠EAP=90°,于是得到∠EAB=∠DAP,即可得到结论;
(2)连接PB,PC,由(1)证得△APD≌△AEB,于是得到PD=AE,∠ADO=∠ABE,推出△ABP≌△DCP,得到PB=PC,根据勾股定理即可得到结论;
(3)过A作AM⊥PE于M,根据等腰直角三角形的性质得到AM=PM=![]() ,求出DM=1+
,求出DM=1+![]() ,由勾股定理得到AD=
,由勾股定理得到AD=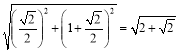 ,于是得到结果.
,于是得到结果.
(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AE⊥AP,
∴∠EAP=90°,
∴∠EAB=∠DAP,
在△APD与△AEB中,
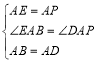 ,
,
∴△APD≌△AEB;
(2)连接PB,PC,由(1)证得△APD≌△AEB,
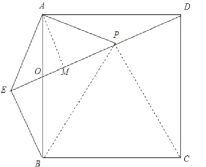
∴PD=AE,∠ADO=∠ABE,
∵AE=AP,
∴PD=AP,
∴∠PAD=∠PDA,
∴∠BAP=∠CDP,
在△ABP与△DCP中,
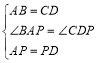 ,
,
∴△ABP≌△DCP,
∴PB=PC,
∵∠BOE=∠AOP,
∴∠BEO=∠BAD=90°,
∵PE=![]() AP=
AP=![]() ,
,
∴PB=![]() ,
,
∴PC=PB=![]() ;
;
(3)过A作AM⊥PE于M,
∴AM=PM=![]() PE=
PE=![]() ,
,
∴DM=1+![]() ,
,
∴AD=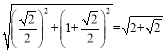 ,
,
∴正方形ABCD的面积=AD![]() =2+
=2+![]() .
.

 考前必练系列答案
考前必练系列答案【题目】已知A、B两个蔬菜市场各有蔬菜14吨,现要全部运往甲、乙两地,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从蔬菜市场A到甲地运费50元/吨,到乙地30元/吨;从蔬菜市场B到甲地运费60元/吨,到乙地45元/吨。
(1)设从蔬菜市场A向甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
蔬菜市场A | x | |
蔬菜市场B |
(2)若总运费为1300元,则从蔬菜市场A向甲地运送蔬菜多少吨?