题目内容
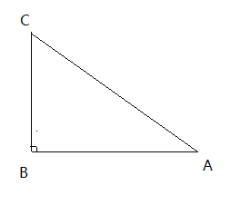
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数![]() 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.

(1)直线AO的解析式;
(2)求反比例函数解析式;
⑶求点C的坐标.
【答案】(1) ![]() ;(2)
;(2)![]() ;(3)(2,4)
;(3)(2,4)
【解析】
试题分析:(1)首先根据三角形的边长求出点A的坐标,再利用待定系数法求出直线AO的解析式;
(2)根据△BOD的面积和OB的长度、∠ABO的度数,求出点D的坐标,再利用待定系数法求出反比例函数的解析式;
(3)解直线![]() 与反比例函数
与反比例函数![]() 构成的方程组求出点C的坐标.
构成的方程组求出点C的坐标.
试题解析:(1)∵OB=4,AB=8,∠ABO=90°
∴A点坐标为(4,8),
设直线AO的解析式为![]()
则![]() ,解得
,解得![]()
即直线AO的解析式为![]() ,
,
(2)∵OB=4,S△BOD=4,∠ABO=90°
∴D点坐标为(4,2),
点D(4,2)代入![]()
则![]() ,解得
,解得![]()
∴反比例函数解析式为![]() ,
,
(3)直线![]() 与反比例函数
与反比例函数![]() 构成方程组为:
构成方程组为: ,
,
解得 ,
, (舍去)
(舍去)
∴C点坐标为(2,4).

练习册系列答案
相关题目