题目内容
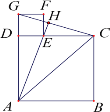
【题目】如图,已知四边形![]() 和四边形
和四边形![]() 为正方形,点
为正方形,点![]() 在线段
在线段![]() 上,点
上,点![]() 在同一直线上,连接
在同一直线上,连接![]() ,并延长
,并延长![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
(3)设![]() ,
,![]() ,当点H是线段GC的中点时,则
,当点H是线段GC的中点时,则![]() 与
与![]() 满足什么样的关系式.
满足什么样的关系式.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() (
( ![]() ).
).
【解析】
(1)先证明△GDC≌△EDA,得∠GCD=∠EAD,推出AH⊥GC;
(2)根据S△AGC=![]() AGDC=
AGDC=![]() GCAH,即可解决问题;
GCAH,即可解决问题;
(3)根据垂直平分线的性质可得结论.
(1)在△GDC和△EDA中,
 ,
,
∴△GDC≌△EDA,
∴∠GCD=∠EAD,
∵∠HEC=∠DEA,
∴∠EHC=∠EDA=90°,
∴AH⊥GC;
(2)∵AD=3,DE=1,
∴GC=AE=![]() ,
,
∵∠DAE+∠AED=90°,∠DEA=∠CEH,
∴∠DCG+∠HEC=90°,
∴∠EHC=90°,
∴AH⊥GC,
∵S△AGC=![]() AGDC=
AGDC=![]() GCAH,
GCAH,
∴![]() ×4×3=
×4×3=![]() ×
×![]() ×AH,
×AH,
∴AH=![]() .
.
(3)由(1)得,AH即GC的中垂线
∴AG=AC (中垂线的性质定理)
∴![]() (
( ![]() )
)

练习册系列答案
相关题目