题目内容
 如图,已知AB为⊙O的弦,OC⊥AB,垂足为C,若OA=10,AB=16,则弦心距OC的长为
如图,已知AB为⊙O的弦,OC⊥AB,垂足为C,若OA=10,AB=16,则弦心距OC的长为
- A.12
- B.10
- C.6
- D.8
C
分析:先求出半弦AC的长,再利用勾股定理即可求出.
解答:在Rt△AOC中,
∵OA=10cm,根据OC⊥AB,则AC= AB=8,
AB=8,
∴OC=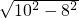 =6.
=6.
故选C.
点评:此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解.
分析:先求出半弦AC的长,再利用勾股定理即可求出.
解答:在Rt△AOC中,
∵OA=10cm,根据OC⊥AB,则AC=
 AB=8,
AB=8,∴OC=
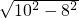 =6.
=6.故选C.
点评:此题涉及圆中求半径的问题,此类在圆中涉及弦长、半径、圆心角的计算的问题,常把半弦长,半圆心角,圆心到弦距离转换到同一直角三角形中,然后通过直角三角形予以求解.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )
22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( ) 如图,已知AB为半⊙O的直径,直线MN与⊙O相切于C点,AE⊥MN于E,BF⊥MN于F.
如图,已知AB为半⊙O的直径,直线MN与⊙O相切于C点,AE⊥MN于E,BF⊥MN于F. 如图,已知AB为⊙O的直径,直线l与⊙O相切于点D,AC⊥l于C,AC交⊙O于点E,DF⊥AB于F.
如图,已知AB为⊙O的直径,直线l与⊙O相切于点D,AC⊥l于C,AC交⊙O于点E,DF⊥AB于F. (2012•包头)如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC,CF,AC.
(2012•包头)如图,已知AB为⊙O的直径,过⊙O上的点C的切线交AB的延长线于点E,AD⊥EC于点D且交⊙O于点F,连接BC,CF,AC. (2012•呼和浩特)如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.
(2012•呼和浩特)如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.