题目内容
梯形ABCD中，AD∥BC，以A为圆心，DA为半径的圆经过B、C、D三点，若AD=5．BC=8，求梯形ABCD的面积．
【答案】分析：过A作AM⊥BC于M点，根据垂径定理得到BM=
BC=4，再在Rt△ABM中，利用勾股定理计算出AM的长，最后利用梯形的面积公式即可得到梯形ABCD的面积．
解答：
解：过A作AM⊥BC于M点，如图：
∴BM=
BC，
而AB=AD=5，BC=8，
∴BM=4，
在Rt△ABM中，AM=
=
=3，
∴S梯形ABCD=
（5+8）×3=
．
点评：本题考查了圆的垂径定理：垂直于弦的直径平分弦，平分弦所对的弧；也考查了勾股定理和梯形的面积公式．
BC=4，再在Rt△ABM中，利用勾股定理计算出AM的长，最后利用梯形的面积公式即可得到梯形ABCD的面积．解答：
解：过A作AM⊥BC于M点，如图：∴BM=
BC，而AB=AD=5，BC=8，
∴BM=4，
在Rt△ABM中，AM=
==3，∴S梯形ABCD=
（5+8）×3=．点评：本题考查了圆的垂径定理：垂直于弦的直径平分弦，平分弦所对的弧；也考查了勾股定理和梯形的面积公式．
练习册系列答案
相关题目
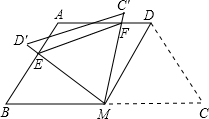如图，等腰梯形ABCD中，AD∥BC，AD=AB=CD=2，∠C=60°，M是BC的中点．
DE．
如图，在梯形ABCD中，AD∥BC，AB=CD，点E在BC的延长线上，且∠BDE=∠ADC．求证：AB•BD=DE•AD．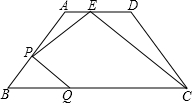
如图，在等腰梯形ABCD中，AD∥BC，AB=5，AD=6，BC=12，点E在AD边上，且AE：ED=1：2，点P是AB边上的一个动点，（P不与A，B重合）过点P作PQ∥CE交BC于点Q，设AP=x，CQ=y，则y与x之间的函数关系是
分别交边CD、BC于点F、E，若AD=3，BC=12，