题目内容
一个等腰梯形,一条对角线长10厘米,顺次连接梯形四边中点,围成的图形是________,这个图形的周长是________.
菱形 20厘米
分析:根据等腰梯形性质得出AC=BD,根据三角形的中位线求出EF= AC,HG=
AC,HG= AC,FG=
AC,FG= BD,HE=
BD,HE= BD,求出EF=FG=HG=EH=5厘米,即可推出菱形EFGH和求出四边形EFGH的周长.
BD,求出EF=FG=HG=EH=5厘米,即可推出菱形EFGH和求出四边形EFGH的周长.
解答: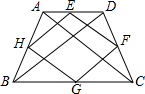
∵四边形ABCD是等腰梯形,AD∥BC,
∴AC=BD=10厘米,
∵E、F、G、H分别是边AD、DC、BC、AB的中点,
∴EF= AC,HG=
AC,HG= AC,FG=
AC,FG= BD,HE=
BD,HE= BD,
BD,
∴EF=FG=HG=EH=5厘米,
∴四边形EFGH是菱形,
四边形EFGH的周长是5厘米+5厘米+5厘米+5厘米=20厘米.
故答案为:菱形,20厘米.
点评:本题考查了等腰梯形性质、三角形的中位线、菱形的判定的应用,关键是求出EF=FG=HG=EH=5厘米,题目比较好,难度不大.
分析:根据等腰梯形性质得出AC=BD,根据三角形的中位线求出EF=
 AC,HG=
AC,HG= AC,FG=
AC,FG= BD,HE=
BD,HE= BD,求出EF=FG=HG=EH=5厘米,即可推出菱形EFGH和求出四边形EFGH的周长.
BD,求出EF=FG=HG=EH=5厘米,即可推出菱形EFGH和求出四边形EFGH的周长.解答:

∵四边形ABCD是等腰梯形,AD∥BC,
∴AC=BD=10厘米,
∵E、F、G、H分别是边AD、DC、BC、AB的中点,
∴EF=
 AC,HG=
AC,HG= AC,FG=
AC,FG= BD,HE=
BD,HE= BD,
BD,∴EF=FG=HG=EH=5厘米,
∴四边形EFGH是菱形,
四边形EFGH的周长是5厘米+5厘米+5厘米+5厘米=20厘米.
故答案为:菱形,20厘米.
点评:本题考查了等腰梯形性质、三角形的中位线、菱形的判定的应用,关键是求出EF=FG=HG=EH=5厘米,题目比较好,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则它们组成一个等腰直角三角形;
,则它们组成一个等腰直角三角形;