题目内容

如图，已知抛物线y=ax²+bx+c（a＜0）与x轴交于A、B两点（点A在点B的右侧），与y轴的正半轴交于点C，以AB为直径的圆经过点C及抛物线上的另一点D，∠ABC=60度．
（1）求点A和点B的坐标（用含有字母c的式子表示）；
（2）如果四边形ABCD的面积为 $数学公式$ ，求抛物线的解析式；
（3）如果当x＞1时，y随x的增大而减小，求c的取值范围．

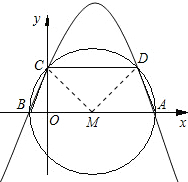解：（1）设线段AB的中点为M，连接CM、DM，由∠ABC=60°，MC=MB，
∴△BCM为等边三角形，
∴由抛物线的对称性可知△ADM也是等边三角形，
又∵MC=MC，∠CMD=180°-60°-60°=60°，
∴△CDM也是等边三角形，
故BC=CD=AD= $\text{[math]}$ AB，
解Rt△BOC得OB= $\text{[math]}$ OC= $\text{[math]}$ c，BC=2OB= $\text{[math]}$ c，
故A（ $\text{[math]}$ c，0），B（- $\text{[math]}$ c，0）；

（2）当S_{四边形ABCD}= $\text{[math]}$ 时， $\text{[math]}$ ×（ $\text{[math]}$ c+ $\text{[math]}$ c）×c= $\text{[math]}$ ，
解得c=1，
∴A（ $\text{[math]}$ ，0），B（- $\text{[math]}$ ，0），C（0，1），
设抛物线解析式y=a（x- $\text{[math]}$ ）（x+ $\text{[math]}$ ），
把A（0，1）代入得a=-1，
∴y=-（x- $\text{[math]}$ ）（x+ $\text{[math]}$ ），
即y=-x²+ $\text{[math]}$ x+1；

（3）如果当x＞1时，y随x的增大而减小，
则对称轴x=- $\text{[math]}$ = $\text{[math]}$ c≤1，c≤ $\text{[math]}$ ，
又∵抛物线交y轴于正半轴，
∴0＜c≤ $\text{[math]}$ ．
分析：（1）取圆心为M，根据抛物线和圆都是轴对称图形，可证明△BCM、△ADM、△CDM都是等边三角形，其中OC是△BCM的高，解直角三角形可得BC长，即为圆的半径，从而可表示A、B两点坐标；
（2）由（1）可得AB= $\text{[math]}$ c，CD= $\text{[math]}$ c，OC=c，根据梯形面积公式求c，可得A、B、C三点坐标，设交点式求抛物线解析式；
（3）当x＞1时，y随x的增大而减小，联想对称轴x=- $\text{[math]}$ = $\text{[math]}$ c≤1，易得c≤ $\text{[math]}$ ，又抛物线交y轴于正半轴，∴0＜c≤ $\text{[math]}$ ．
点评：本题考查了圆与抛物线的综合运用，要求会用对称性，特殊三角形解答本题，也要熟练掌握解直角三角形的知识．