题目内容
如图所示,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.
∠C=
（∠1+∠2）或∠1+∠2=2∠C （1分）
理由如下：由折叠可得 ∠C′EF=∠CEF
∠C′F′E=∠CEF （2分）
∴∠1+2∠CEF=180°（3分）
∠2+2∠CEF=180°（4分）
∴2∠CEF+2∠CEF=360°-（∠1+∠2）
又∠CEF+∠CFE=180°-（∠1+∠2）
又∠CEF+∠CFE=180°-∠C ∴∠C=（∠1+∠2）（8分）解析:
因为△EC′F是△ECF折叠而成的，所以∠CEF=∠C′EF，∠CFE=∠EFC′，故∠1=180°-2∠CEF，∠2=180°-2∠CFE，即∠1+∠2=2∠C
（∠1+∠2）或∠1+∠2=2∠C （1分）理由如下：由折叠可得 ∠C′EF=∠CEF
∠C′F′E=∠CEF （2分）
∴∠1+2∠CEF=180°（3分）
∠2+2∠CEF=180°（4分）
∴2∠CEF+2∠CEF=360°-（∠1+∠2）
又∠CEF+∠CFE=180°-
（∠1+∠2）又∠CEF+∠CFE=180°-∠C ∴∠C=
（∠1+∠2）（8分）解析:因为△EC′F是△ECF折叠而成的，所以∠CEF=∠C′EF，∠CFE=∠EFC′，故∠1=180°-2∠CEF，∠2=180°-2∠CFE，即∠1+∠2=2∠C
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
△A1B1C1绕点O旋转180°后得到△A2B2C2．
17、如图所示，将△ABC平移，可以得到△DEF，点B的对应点为点E，请画出点A的对应点D、点C的对应点F的位置，并做出△DEF．
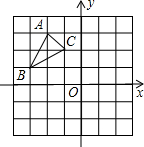
△ABC在平面直角坐标系中的位置如图所示．将△ABC向右平移6个单位得到△A1B1C1，再将△A1B1C1向下平移4个单位得到△A2B2C2，请画出△A1B1C1和△A2B2C2，并写出点C2的坐标．