题目内容

⊙O的半径为6，⊙O的一条弦长4
5
，以4为半径的同心圆与此弦的位置关系是（　　）
A．相离B．相交C．相切D．不确定
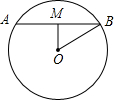
如图，已知：AB=4
5
，OB=6，
∵M为AB中点，
∴AM=BM=2
5
，
根据勾股定理可知：OM=
OB2-BM2
=
36-20
=
16
=4，
∴以4为半径的同心圆与此弦的位置关系是：相切．
故选C．
练习册系列答案
相关题目
如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，DE⊥AC，垂足为点E．
（1）求证：直线DE与⊙O相切；
（2）当AB=9，BC=6时，求线段DE的长．
在Rt△ABC中，∠C=90°，BC=5，AC=12，若以C为圆心，R为半径作的圆与斜边AB没有公共点，则R的取值范围是______．
如图，AB是⊙O的直径，BC交⊙O于点D，DE⊥AC于点E，要使DE是⊙O的切线，还需补充一个条件，则补充的条件不正确的是（　　）
A．DE=DOB．AB=ACC．CD=DBD．AC∥OD
如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB．
（1）求证：PC是⊙O的切线；
（2）求∠P的度数；
（3）点M是弧AB的中点，CM交AB于点N，AB=4，求线段BM、CM及弧BC所围成的图形面积．
如图，P是⊙O的直径CB延长线上的一点，PA是⊙O的切线，切点为A，∠P=20°，则∠ABP=______度．
已知⊙O过点D（4，3），点H与点D关于y轴对称，过H作⊙O的切线交y轴于点A（如图1）．
（1）求⊙O半径；
（2）sin∠HAO的值；
（3）如图2，设⊙O与y轴正半轴交点P，点E、F是线段OP上的动点（与P点不重合），连接并延长DE，DF交⊙O于点B，C，直线BC交y轴于点G，若△DEF是以EF为底的等腰三角形，试探索sin∠CGO的大小怎样变化？请说明理由．
如图，在Rt△ABC中，∠C=90°，O、D分别为AB、BC上的点．经过A、D两点的⊙O分别交AB、AC于点E、F，且D为
EF
的中点．
（1）求证：BC与⊙O相切；
（2）当AD=2
3
，∠CAD=30°时．求
AD
的长．
如图．若△ABC的BC边上的高为AH，BC长为30cm，DE∥BC，以DE为直径的半圆与BC切于F，若此半圆的面积是18πcm2，则AH=______cm．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网