题目内容
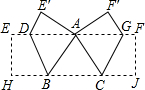如图，长方形纸带EFJH沿着DB、GC折叠，使点H，点J都落在线段EF上的点A处，已知△ABC是边长为4的等边三角形，则DE的长为2
2
．分析：由题给条件及图形可知：AB=HB=BC=AC=CJ=AD=AG=4，继而求得HJ的长，又DE=GF，继而求得DE的长．
解答：解：由翻折的性质可知：∠ABD=∠HBD，∠ACG=∠JCG，
又△ABC是边长为4的等边三角形，
∴∠ABC=∠ACB=60°，
∴∠ABD=∠ACG=60°，∠BAD=∠CAG=60°，
∴△ABD和△ACG为等边三角形，
∴AB=HB=BC=AC=CJ=AD=AG=4
∴DE+GF=HJ-（AD+AG）=3×4-2×4=4，
又DE=GF，
∴DE=2．
故答案为：2．
又△ABC是边长为4的等边三角形，
∴∠ABC=∠ACB=60°，
∴∠ABD=∠ACG=60°，∠BAD=∠CAG=60°，
∴△ABD和△ACG为等边三角形，
∴AB=HB=BC=AC=CJ=AD=AG=4
∴DE+GF=HJ-（AD+AG）=3×4-2×4=4，
又DE=GF，
∴DE=2．
故答案为：2．
点评：本题考查翻折变换的知识，注意掌握折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，只是位置变化．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
