题目内容
观察计算:
当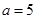 ,
,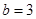 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.
当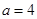 ,
,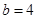 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.
探究证明:
如图所示,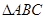 为圆O的内接三角形,
为圆O的内接三角形,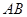 为直径,过C作
为直径,过C作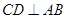 于D,设
于D,设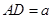 ,BD=b.
,BD=b.

(1)分别用 表示线段OC,CD;
表示线段OC,CD;
(2)探求OC与CD表达式之间存在的关系(用含a,b的式子表示).
归纳结论:
根据上面的观察计算、探究证明,你能得出 与
与 的大小关系是:______________.
的大小关系是:______________.
实践应用:
要制作面积为4平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
当
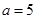 ,
,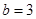 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.当
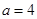 ,
,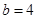 时,
时, 与
与 的大小关系是_________________.
的大小关系是_________________.探究证明:
如图所示,
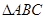 为圆O的内接三角形,
为圆O的内接三角形,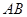 为直径,过C作
为直径,过C作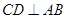 于D,设
于D,设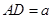 ,BD=b.
,BD=b.
(1)分别用
 表示线段OC,CD;
表示线段OC,CD;(2)探求OC与CD表达式之间存在的关系(用含a,b的式子表示).
归纳结论:
根据上面的观察计算、探究证明,你能得出
 与
与 的大小关系是:______________.
的大小关系是:______________.实践应用:
要制作面积为4平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
观察计算:当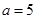 ,
,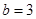 时,
时, >
> ;当
;当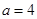 ,
,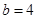 时,
时, =
= .
.
探究证明:(1)OC= ,
,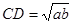 ;
;
(2)当a=b时,OC=CD, =
= ;a≠b时,OC>CD,
;a≠b时,OC>CD, >
> .
.
结论归纳:
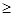
 .
.
实践应用:周长最小为4米.
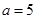 ,
,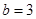 时,
时, >
> ;当
;当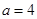 ,
,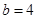 时,
时, =
= .
.探究证明:(1)OC=
 ,
,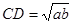 ;
;(2)当a=b时,OC=CD,
 =
= ;a≠b时,OC>CD,
;a≠b时,OC>CD, >
> .
.结论归纳:

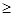
 .
.实践应用:周长最小为4米.
试题分析:观察计算:把
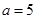 ,
,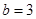 和
和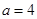 ,
,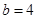 分别代入
分别代入 与
与 计算,即可作出判断;
计算,即可作出判断;探究证明:(1)由于OC是直径AB的一半,则OC易得.通过证明△ACD∽△CBD,可求CD;
(2)分a=b,a≠b讨论可得出
 与
与 的大小关系;
的大小关系;实践应用:通过前面的结论长方形为正方形时,周长最小.
试题解析:观察计算:当
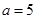 ,
,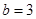 时,
时, >
>
当
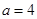 ,
,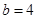 时,
时, =
= .
.探究证明:
(1)∵AB=AD+BD=2OC,
∴OC=

∵AB为⊙O直径,
∴∠ACB=90°.
∵∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD.
∴△ACD∽△CBD.
∴
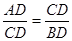 .即CD2=AD•BD=ab,解得
.即CD2=AD•BD=ab,解得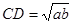 ;
;(2)当a=b时,OC=CD,
 =
= ;
;a≠b时,OC>CD,
 >
> .
.结论归纳:

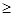
 .
.实践应用
设长方形一边长为x米,则另一边长为
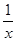 米,设镜框周长为l米,
米,设镜框周长为l米,则
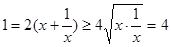 ,当
,当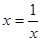 ,即x=1(米)时,镜框周长最小.
,即x=1(米)时,镜框周长最小.此时四边形为正方形时,周长最小为4米.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
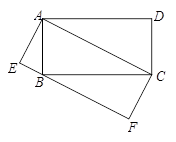
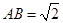 ,AD=2,∠B=45°,
,AD=2,∠B=45°,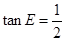 ,求CF的长.
,求CF的长.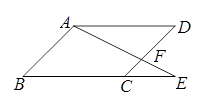
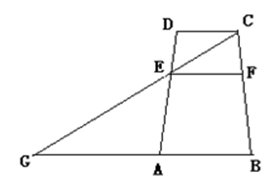

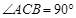 ,
,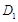 是斜边AB的中点,过
是斜边AB的中点,过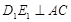 于
于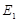 ,连结
,连结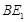 交
交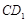 于
于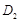 ;过
;过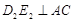 于
于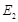 ,连结
,连结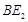 交
交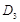 ;过
;过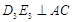 于
于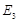 ,…,如此继续,可以依次得到点
,…,如此继续,可以依次得到点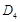 ,
,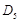 …,
…,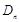 ,分别记
,分别记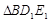 ,
,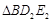 ,
,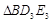 ,…,
,…,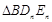 的面积为
的面积为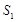 ,
,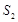 ,
,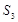 ,…
,…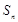 ,则
,则 .
.
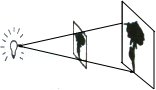
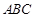 中,
中,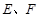 分别是
分别是 边上的点,
边上的点,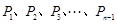 是
是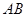 边的
边的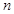 等分点,
等分点,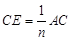 ,
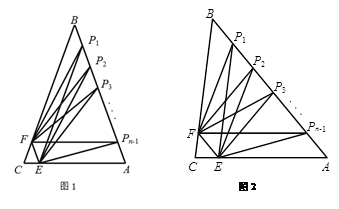
,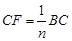 .如图1,若
.如图1,若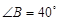 ,
,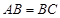 ,则∠
,则∠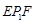 +∠
+∠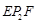 +∠
+∠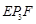 +
+ 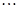 +∠
+∠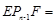 度;如图2,若
度;如图2,若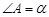 ,
,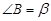 ,则∠
,则∠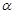 ,
,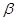 的式子表示).
的式子表示).