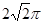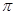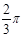题目内容
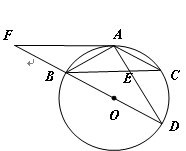
如图,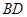 为⊙
为⊙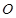 的直径,
的直径,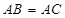 ,
,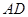 交
交 于点
于点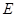 ,
,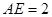 ,
,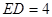 .
.
(1)求证: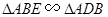 ;
;
(2)求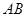 的长;
的长;
(3)延长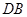 到
到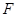 ,使得
,使得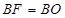 ,连接
,连接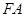 ,试判断直 线
,试判断直 线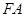 与⊙
与⊙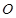 的位置关系,并说明理由.
的位置关系,并说明理由.
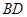 为⊙
为⊙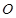 的直径,
的直径,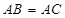 ,
,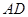 交
交 于点
于点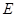 ,
,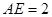 ,
,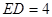 .
.
(1)求证:
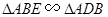 ;
;(2)求
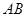 的长;
的长;(3)延长
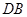 到
到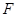 ,使得
,使得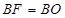 ,连接
,连接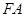 ,试判断直 线
,试判断直 线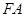 与⊙
与⊙ 的位置关系,并说明理由.
的位置关系,并说明理由. 解:(1)证明:∵AB=AC,
∴∠ABC=∠C, …………1分
∵∠C=∠D,
∴∠ABC=∠D, …………2分
又∵∠BAE=∠EAB,
∴△ABE∽△ADB, …………3分
(2) ∵△ABE∽△ADB,
∴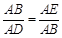 , …………4分
, …………4分
∴AB2=AD·AE=(AE+ED)·AE=(2+4)×2=12 …………5分
∴AB=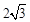 .…………6分
.…………6分
(3) 直线FA与⊙O相切,理由如下:
连接OA, …………7分
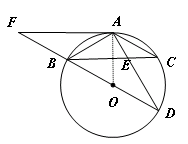
∵BD为⊙O的直径,
∴∠BAD=90°,
∴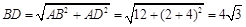 ,
,
BF=BO=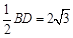 ,…………8分
,…………8分
∵AB=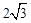 ,
,
∴BF=BO=AB,可证∠OAF=90°,
∴直线FA与⊙O相切.…………10分
∴∠ABC=∠C, …………1分
∵∠C=∠D,
∴∠ABC=∠D, …………2分
又∵∠BAE=∠EAB,
∴△ABE∽△ADB, …………3分
(2) ∵△ABE∽△ADB,
∴
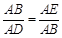 , …………4分
, …………4分∴AB2=AD·AE=(AE+ED)·AE=(2+4)×2=12 …………5分
∴AB=
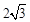 .…………6分
.…………6分 (3) 直线FA与⊙O相切,理由如下:
连接OA, …………7分

∵BD为⊙O的直径,
∴∠BAD=90°,
∴
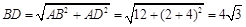 ,
,BF=BO=
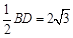 ,…………8分
,…………8分∵AB=
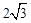 ,
,∴BF=BO=AB,可证∠OAF=90°,
∴直线FA与⊙O相切.…………10分
(1)根据AB=AC,可得∠ABC=∠C,利用等量代换可得∠ABC=∠D然后即可证明△ABE∽△ADB.
(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.
(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可
(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.
(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可

练习册系列答案
相关题目
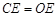 ;③△ODE∽△ADO;④
;③△ODE∽△ADO;④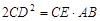 .其中一定正确的结论有( )
.其中一定正确的结论有( )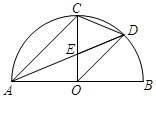
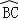 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.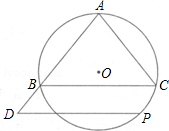
 .
. ;
;